Abstract
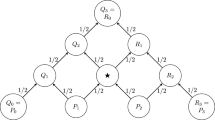
In many applications of the finite element method, the explicit form of the basis functions is not known. A well-known exception is that of piecewise linear approximation over a triangulation of the plane, where the basis functions are pyramid functions. In the present paper, the basis functions are displayed in closed form for piecewise polynomial approximation of degreen over a triangulation of the plane. These basis functions are expressed simply in terms of the pyramid functions for linear approximation.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J. H. Argyris, I. Fried and D. W. Scharpf,The TET 20 and TEA 8 Elements for the Matrix Displacement Method, The Aeronautical Journal of the Royal Aeronautical Society 72 (1968), 618–623.
C. A. Felippa and R. W. Clough,The Finite Element Method in Solid Mechanics, contributed to Numerical Solution of Field Problems in Continuum Physics, SIAM-AMS Proceedings Vol. 2 (1970).
M. J. L. Hussey, R. W. Thatcher and M. J. M. Bernal,On the Construction and Use of Finite Elements, J. Inst. Maths. Applics. 6 (1970), 263–282.
R. A. Nicolaides,On Lagrange Interpolation in n Variables, Technical Note I. C. S. I. 274, Institute of Computer Science, University of London (1970).
P. Silvester,Symmetric Quadrature Formulae for Simplexes, Math. of Comp. 24 (1970), 95–100.
J. L. Synge,The Hypercircle in Mathematical Physics, Cambridge University Press (1957).
M. Zlamal,On the Finite Element Method, Numer. Math. 12 (1968), 394–409.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Mitchell, A.R., Phillips, G.M. Construction of basis functions in the finite element method. BIT 12, 81–89 (1972). https://doi.org/10.1007/BF01932676
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01932676