Skip to main content
SpringerLink
Log in

On some topological properties of numerical algorithms

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

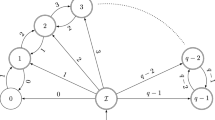
A result quantity in a numerical algorithm is considered as a function of the input data, roundoff and truncation errors. In order to investigate this functional relationship using the methods of mathematical analysis a structural model of the numerical algorithm calledR-automaton is introduced. It is shown that the functional dependence defined by anR-automaton is a continuous rational function in a neighborhood of any data point except in a point set, the Lebesgue measure of which is zero. An effective general-purpose algorithm is presented to compute the derivative of any result quantity with respect to the individual roundoff and truncation errors. Some ways of generalizing theR-automation model without losing the results achieved are finally suggested.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. Bjørner,Flowchart machines, BIT 10 (1970), 415–442.

    Google Scholar 

  2. P. Henrici,Elements of Numerical analysis, Wiley, New York, 1964.

    Google Scholar 

  3. E. Isaacson and H. B. Keller,Analysis of numerical methods, Wiley, New York, 1966.

    Google Scholar 

  4. E. Kamke,Das Lebesgue-Stieltjes Integral, B. G. Teubner Verlagsgesellschaft, Leipzig 1956.

    Google Scholar 

  5. D. Knuth,The art of computer programming, vol. 2, Seminumerical algorithms, Addison-Wesley, Reading, Massachusetts, 1969.

    Google Scholar 

  6. S. Linnainmaa,The representation of the cumulative roundoff error of an algorithm as a Taylor-expansion of individual roundoff errors, (In Finnish language), Master's thesis, University of Helsinki, Computer Science Department, 1970.

  7. R. E. Moore,Interval analysis, Prentice Hall, Englewood Cliffs, N.J., 1966.

    Google Scholar 

  8. M. Tienari,A statistical model of roundoff error for varying length floating-point arithmetic, BIT 10 (1970), 355–365.

    Google Scholar 

  9. M. V. Wilkes,The outer and inner syntax of a programming language, Computer Journal 11 (1968), 260–263.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computer Science Department, University of Helsinki, Töölönkatu 11, SF-00100, Helsinki 10, Finland

    Martti Tienari

Authors
  1. Martti Tienari
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tienari, M. On some topological properties of numerical algorithms. BIT 12, 409–433 (1972). https://doi.org/10.1007/BF01932311

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01932311

Keywords

Search

Navigation