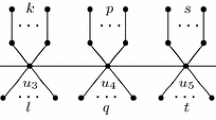
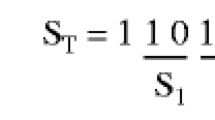Abstract
2–3 brother trees form a dense class of search trees havingO(logN) insertion and deletion algorithms. In this paper we provide anO(logN) insertion algorithm and show that these trees have much better density and storage utilization than 2–3 trees. Thus we demonstrate that the “brother property” which has so far been used only for binary trees can be usefully applied to 2–3 trees.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. V. Aho, J. E. Hopcroft, and J. D. Ullman,The design and analysis of computer algorithms, Addison-Wesley, Reading (1974).
D. E. Knuth,The art of computer programming, Vol. III: Sorting and searching, Addison-Wesley, Reading (1973).
H. P. Kriegel, V. K. Vaishnavi, and D. Wood, 2–3brother trees, Computer Science Technical Report 78-CS-6, Department of Applied Mathematics, McMaster University, Hamilton, (1978).
Th. Ottmann and D. Wood, 1–2brother trees, Computer Journal (1978), to appear.
V. K. Vaishnavi, H. P. Kriegel, and D. Wood,Height balanced 2–3trees, Computing (1978), to appear.
A. C.-C. Yao,On random 2–3trees, Acta Informatica 9 (1978), 159–170.
Author information
Authors and Affiliations
Additional information
Work supported partially by a Natural Sciences and Engineering Research Council of Canada Grant No. A-7700 and partially by the German Academic Exchange Service under Nato Research Grant No. 430/402/584/8.
Rights and permissions
About this article
Cite this article
Kriegel, H.P., Vaishnavi, V.K. & Wood, D. 2–3 brother trees. BIT 18, 425–435 (1978). https://doi.org/10.1007/BF01932021
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01932021