Interior layer phenomena of semilinear systems

Abstract

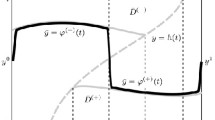
In this paper, we study the interior layer phenomena of singular perturbation boundary value problems for semilinear systems:

$$\begin{gathered} \varepsilon y = f\left( {t, y, \varepsilon } \right) \left( {a< t< b} \right) \hfill \\ y\left( {a, \varepsilon } \right) = A\left( \varepsilon \right), y\left( {b, \varepsilon } \right) = B\left( \varepsilon \right) \hfill \\ \end{gathered} $$

where ɛ>0 is a small parameter, y, f, A and B are n-dimensional vector functions. This vector boundary value peoblem does not appear to have been studied, although the scalar boundary problem has been treated extensively. Under appropriate assumptions we obtain existence of solution as in the scalar problem and the estimate of this solution in terms of appropriate inequalities as well.