Abstract
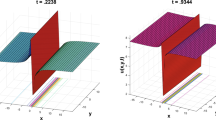
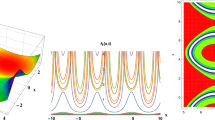
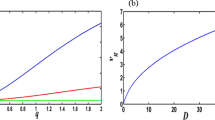
This paper reports a type of laws which governs action potential of nervous impulses, and it is discussed by general form —nonlinear dispersive process. We find that the nervous wave is a slowly varying amplitude solitary wave in the small dispersive case. We prove that the solitary wave is not generated in the ordinary dispersion, but a travelling wave with varying amplitudes may be obtained. The stability of various possible action potentials and bifurcation in overdamped case are also discussed in this paper.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Maximow, A. A., William Bloom and D. W. Fawcett, A Textbook of Histology, 9th ed. (1968).
Tribe, Michael A. and Michael R. Eraut, Nerves and Muscle, (1977).
Hodgkin, A.L., and A.F. Huxley, J. Physiol, 128:28, (1955), 117:500, (1952).
Haken, Hermann, Synergetics, (1977).
Author information
Authors and Affiliations
Additional information
Communicated by Yang Gui-tong.
Rights and permissions
About this article
Cite this article
Wen-liang, T. One type of solutions of conduction of nervous pulses and the stability of action potential. Appl Math Mech 4, 117–126 (1983). https://doi.org/10.1007/BF01896719
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01896719