Skip to main content
SpringerLink
Log in

Minimizing distortion and internal forces in truss structures via simulated annealing

  • Originals
  • Published:
Structural optimization Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

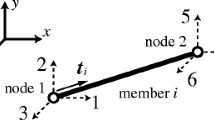
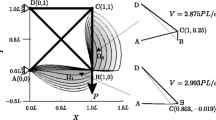
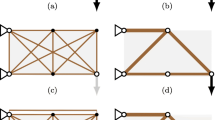
Abstract

Inaccuracies in the length of members and the diameters of joints of large space structures may produce unacceptable levels of surface distortion and internal forces. We formulate two discrete optimization problems, one to minimize surface distortion (DRMS) and the other to minimize internal forces (FRMS). Both of these problems are based on the influence matrices generated by a small deformation linear analysis. Good solutions are obtained for DRMS and FRMS through the use of a simulated annealing heuristic. Results based on two biobjective (DRMS and FRMS) optimization models are discussed

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Aarts, E.H.L.; Van Laarhoven, P.J.M. 1985: Statistical cooling: a general approach to combinatorial optimization problems.Phillips J. Research 40, 193–226

    Google Scholar 

  • Burkard, R.E. 1984: Quadratic assignment problems.European J. Operational Research 15, 283–289

    Article  MathSciNet  Google Scholar 

  • Burkard, R.E.; Fincke, U. 1983: The asymptotic probabilistic behaviour of quadratic sum assignment problems.Zeitschrift für Operations Research 27, 73–81

    Article  Google Scholar 

  • Burkard, R.E.; Rendl, F. 1984: A thermodynamically motivated simulation procedure for combinatorial optimization problems.European J. Operational Research 17, 169–174

    Article  Google Scholar 

  • Cerny, V. 1985: Thermodynamical approach to the traveling salesman problem: an efficient simulation algorithm.J. Optimiz. Theory Appl. 45, 41–52

    Article  Google Scholar 

  • Collins, N.E.; Eglese, R.W.; Golden, B.L. 1988: Simulated annealing- an annotated bibliography.Amer. J. Math. & Management Sci. 8, 209–308

    Google Scholar 

  • Elperin, T. 1988: Monte Carlo structural optimization in discrete variables with annealing algorithm.Int. J. Num. Meth. Eng. 26, 815–821

    Google Scholar 

  • Eschenauer, H.; Koski, J.; Osyczka, A. 1990:Multicriteria design optimization, procedures, and applications. Berlin, Heidelberg, New York: Springer

    Google Scholar 

  • Garey, M.R.; Johnson, D.S. 1979:Computers and intractability: a guide to the theory of NP-completeness. New York: W.H. Freeman and Company

    Google Scholar 

  • Greene, W.H. 1985: Effects of random member length errors on the accuracy and internal loads of truss antennas.J. Spacecraft and Rockets

  • Greene, W.H.; Haftka, R.T. 1989: Reducing distortion and internal forces in truss structures by member exchanges.NASA Technical Memorandum 101535

  • Johnson, D.S.; Aragon, C.R.; McGeoch, L.A.; Schevon, C. 1990: Optimization by simulated annealing: an experimental evaluation. Part I, graph partitioning.Operations Research 37, 865–893

    Google Scholar 

  • Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. 1983: Optimization by simulated annealing.Science 220, 671–680

    Google Scholar 

  • Koopmans, T.C.; Beckmann, M.J. 1957: Assignment problems and the location of economic activities.Econometrica 25, 52–76

    Google Scholar 

  • Koski, J. 1985: Defectiveness of weighting method in multicriterion optimization of structures.Comm. Appl. Num. Meth. 1, 333–337

    Google Scholar 

  • Lundy, M.; Mees, A. 1986: Convergence of an annealing algorithm.Math. Prog. 34, 111–124

    Article  Google Scholar 

  • Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E. 1953: Equation of state calculations by fast computing machines.J. Chem. Phys. 21, 1087–1092

    Article  Google Scholar 

  • Press, H.P.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. 1986:Numerical recipes: the art of scientific computing. New York: Cambridge University Press

    Google Scholar 

  • Salama, M.; Bruno, R.; Chen, G.-S.; Garba, J. 1988: Optimal placement of excitations and sensors by simulated annealing. In:Proc. Recent advances in multidisciplinary analysis and optimization, NASA CP-3031, 1441–1458

  • Seneta, E. 1981:Non-negative matrices and Markov chains. 2nd edition, Berlin, Heidelberg, New York: Springer

    Google Scholar 

  • Stadler, W. 1988: Multicriteria optimization in engineering and in the sciences.37. In:Mathematical concepts and methods in science and engineering. New York: Plenum Press

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, College of William and Mary, 23185, Williamsburg, VA, USA

    R. K. Kincaid

Authors
  1. R. K. Kincaid
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kincaid, R.K. Minimizing distortion and internal forces in truss structures via simulated annealing. Structural Optimization 4, 55–61 (1992). https://doi.org/10.1007/BF01894081

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01894081

Keywords

Search

Navigation