Abstract
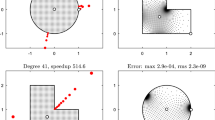
Letg be the function which maps conformally a rectangleR onto a simply connected domainG so that the four vertices ofR are mapped respectively onto four specified pointsz 1,z 2,z 3,z 4 on∂G. This paper is concerned with the study of a domain decomposition method for computing approximations tog and to an associated domain functional in cases where: (i)G is bounded by two parallel straight lines and two Jordan arcs. (ii) The four pointsz 1,z 2,z 3,Z 4, are the corners where the two straight lines meet the two arcs.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
N. V. Challis, D. M. Burley (1982):A numerical method for conformal mapping. IMA J. Numer. Anal.,2:169–181.
D. Gaier (1964): Konstruktive Methoden der konformen Abbildung. Berlin: Spring-Verlag.
D. Gaier (1972):Ermittlung des konformen Moduls von Vierecken mit Differenzenmethoden. Numer. Math.,19:179–194.
D. Gaier, F. Huckemann (1962):Extremal problems for functions schlicht in an annulus. Arch. Rational Mech. Anal.,9:415–421.
D. Gaier, N. Papamichael (1987):On the comparison of two numerical methods for conformal mapping. IMA J. Numer. Anal.,7:261–282.
I. E.Garrick (1936): Potential Flow about Arbitrary Biplane Wing Sections. NACA Report 542.
G. Hardy, J. E. Littlewood, G. Pólya (1952): Inequalities, 2nd edn. Cambridge: Cambridge University Press.
P. Henrici (1986): Applied and Computational Complex Analysis, Vol. III. New York: Wiley.
L. H. Howell, L. N. Trefethen (1990):A modified Schwarz-Christoffel transformation for elongated regions. SIAM J. Sci. Statist. Comput.,11:928–949.
K. Menke (1987):Distortion theorems for functions schlicht in an annulus. J. Reine Angew Math.,375/376:347–361.
C. D. Mobley, R. J. Stewart (1980):On the numerical generation of boundary-fitted orthogonal curvilinear coordinate systems. J. Comput. Phys.,34:124–135.
N. Papamichael (1989):Numerical conformal maping onto a rectange with applications to the solution of Laplacian problems. J. Comput Appl. Math.,28:63–83.
N. Papamichael, C. A. Kokkinos, M. K. Warby (1987):Numerical techniques for conformal mapping onto a rectangle. J. Comput Appl. Math.,20:349–358.
N. Papamichael, N. S. Stylianopoulos (1990):On the numerical performance of a domain decomposition method for conformal mapping. In: Computational Methods and Function Theory (St. Ruscheweyh, E. B. Saff, L. C. Salinas, R. S. Varga, eds.). Lecture Notes in Mathematics, vol. 1435. Berlin: Springer-Verlag, pp. 155–169.
A. Seidl, H. Klose (1985):Numerical conformal mapping of a towel-shaped region onto a rectangle. SIAM J. Sci. Statist. Comput.,6:833–842.
L. N. Trefethen, ed. (1986): Numerical Conformal Mapping. Amsterdam: North-Holland. (Reprinted from (1986): J. Comput. Appl. Math.,14:1–269).
J. J. Wanstrath, R. E. Whitaker, R. O. Reid, A. C. Vastano (1976): Storm Surge Simulation in Transformed Co-ordinates. Technical Report 76-3, U. S. Coastal Engineering Research Center, Fort Belvoir, VA.
S. E. Warschawski (1945):On Theodorsen's method of conformal mapping of nearly circular regions. Quart. Apply. Math.,3:12–28.
Author information
Authors and Affiliations
Additional information
Communicated by Dieter Gaier.
Rights and permissions
About this article
Cite this article
Papamichael, N., Stylianopoulos, N.S. A domain decomposition method for conformal mapping onto a rectangle. Constr. Approx 7, 349–379 (1991). https://doi.org/10.1007/BF01888163
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01888163