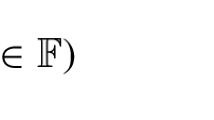On products of additive functions

Summary

During the 1991 Debrecen-Graz Seminar on Functional Equations, L. Székelyhidi posed the following problem:

Suppose thata ₁,a ₂,...,a _n are additive functions from an abelian groupG to ℂ, and assume that we have

$$a_1 (t) \cdot a_2 (t) \cdot \ldots \cdot a_n (t) = 0(t \in G).$$

Is it then true that there existsa j ∈ {1,...,n} such thata _j = 0?

In this paper two generalizations of this question are considered and answered positively. LetG be an abelian group and

be a field of characteristic 0. Then the following is shown.

Theorem 1. Let

be additive functions. Let 1 ⩽r ⩽s be such thata ₁ ...,a _r are linearly independent, and

$$a_j = \sum\limits_{p = 1}^r {\lambda _{j\rho } a_p } (j = r + 1, \ldots ,s),$$

whereλ _jρ ∈

. Let

be the ideal generated by the linear forms

$$h_j = X_j - \sum\limits_{p = 1}^r {\lambda _{jp} X_p } (j = r + 1, \ldots ,s).$$

Then

is a prime ideal and consists of all

satisfying

$$f(a_1 (x), \ldots ,a_s (x)) = 0(x \in G).$$

In particular, if T ₁,...,T _m ∈

are polynomials satisfying

$$(T_1 \cdot \ldots \cdot T_m )(a_1 (x), \ldots ,a_s (x)) = 0(x \in G)$$

then there is an index 1 ⩽l ⩽m such that

$$T_1 (a_1 (x), \ldots ,a_s (x)) = 0(x \in G).$$

Calling a function

a generalized polynomial if for somen and allh ∈ G then-th differenceΔ ⁿ _h p vanishes and denoting by

the ring of those polynomials, the following theorem is shown.

Theorem 2.

is an integral domain.