Abstract
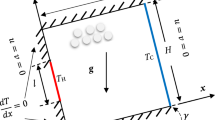
An experimental and analytical investigation pertaining to the effect of density inversion on steady free convective heat transfer of water in a confined rectangular vessel in which different temperatures are imposed on the opposing vertical walls is carried out. Water, as a testing fluid, has its maximum density at 4‡C. Temperature of the cold wall is maintained at 0‡C, while that of the hot wall is varied from 1‡C to 12‡ C. Photographs and analytical descriptions of the flow patterns, temperature distributions and average Nusselt number are presented. Moreover, the effect of dimensions of a rectangular vessel on the average Nusselt number is investigated. From the present investigation, it can be demonstrated both experimentally and analytically that the density inversion of water have an influential effect on the free convection heat transfer in the prescribed water layer, moreover, the average Nusselt number is a peculiar function of temperature difference between the cold and the hot walls, unlike the previous results for common fluids without density inversion.
Zusammenfassung
Der Einflu\ der Dichteumkehr von Wasser auf die stationÄre freie Konvektion in einem geschlossenen rechtwinkligen BehÄlter, dessen gegenüberliegende senkrechte WÄnde auf verschiedenen Temperaturen gehalten werden, ist experimentell und analytisch untersucht. Wasser hat sein Dichtemaximum bei 4‡C. Die kalte Wand ist auf 0‡C gehalten, die Temperatur der warmen Wand liegt zwischen 1‡C und 12‡C. Die Strömungsform, die Temperaturverteilung und die mittlere Nu\elt-Zahl werden durch photographische Aufnahmen und analytische Rechnungen beschrieben. Auch der Einflu\ der BehÄlterdimensionen auf die mittlere Nu\eltZahl ist angegeben. Es zeigt sich, da\ die Dichteumkehr den WÄremübergang in der Wasserschicht grundsÄtzlich verÄndern kann und da\ die Nu\elt-Zahl in eigentümlicher Weise vom angelegten TemperaturgefÄlle abhÄngt, im Gegensatz zu Älteren Ergebnissen für übliche Flüssigkeiten ohne Dichteumkehr.
Similar content being viewed by others
Abbreviations
- Gr:
-
Grashof number, gW3/Ν 2c
- H:
-
height of rectangular vessel
- Nu:
-
average Nusselt number, defined as Eq. (11)
- Nu* :
-
average Nusselt number, qW/λδT
- Pr:
-
Prandtl number, Νc/α c
- q:
-
heat flux at wall
- Ra* :
-
Rayleigh number, g ¦Β¦δTW3/Να
- T:
-
temperature
- δT:
-
temperature difference, Th-Tc(=Th)
- u′, v′:
-
velocity components
- u,v:
-
non-dimensional velocity components, (u′,v′)W(√Gr Ν c )
- x′,y′:
-
coordinates
- x,y:
-
non-dimensional coordinates, (x′,y′)/W
- W:
-
width of rectangular vessel
- α :
-
thermal diffusivity
- Β:
-
coefficient of cubical expansion
- θ:
-
non-dimensional temperature,(T-Tc)/(Th-Tc)
- и:
-
thermal conductivity
- и* :
-
non-dimensional thermal conductivity, и/иc
- Μ:
-
viscosity
- Μ* :
-
non-dimensional viscosity, Μ/Μc
- Ν :
-
kinematic viscosity
- Ν* :
-
non-dimensional kinematic viscosity, Ν/Νc
- ρ:
-
density
- ρ* :
-
non-dimensional density, ρ/ρc
- ψ:
-
stream function, defined as Eq. (3)
- ψ:
-
non-dimensional stream function, ψ/(√Gr Νc)
- Ω:
-
vorticity, defined as Eq. (2)
- Ω:
-
non-dimensional vorticity, ΩW 2(√Gr Ν c )
- c:
-
refers to cold wall
- h:
-
refers to hot wall
Literature
Batchelor, G.K.: Heat transfer by free convection across a closed cavity between vertical boundary at different temperatures. Quart. J. Mech. Appl. Math.12, (1954) 209–233
Eckert, E.R.G.; Carson, W.O.: Natural convection in an air layer enclosed between two vertical plates with different temperatures. Int. J. Heat Mass Trans.2, (1961) 106–120
Dropkin, D.; Somerscales, E.: Heat transfer by natural convection in liquid confined by two parallel plates which are inclined at various angles with respect to the horizontal. J. Heat Transfer87C (1965) 77–84
Emery, A.F.; Chu, N.C.: Heat transfer across vertical layers. J. Heat Transfer87C (1965) 110–114
MacGregor, R.K.; Emery, A.F.: Free convection through vertical plane layers moderate and high Prandtl number fluids. J. Heat Transfer91C, (1969) 391–403
Chu, H.H.S.; Churchill, S.W.; Patterson, C.V. S.: The effect of heater size, location, aspect ratio, and boundary conditions on two dimensional, laminar, natural convection in rectangular channels. J. Heat Transfer98C, (1976) 194–201
Dumoré, J.M.; Merk, H.J.; Prins, J.A.: Heat transfer from water to ice by thermal condition. Nature, Lond.172 (1953) 480–461
Merk, H.J.: The influence of melting and anomalous expansion on the thermal convection in laminar boundary layer. Appl. Scient. Res.4 (1953) 435–452
Ede, A.J.: The influence of anomalous expansion on natural convection in water. Appl. Scient. Res.5, (1955) 458–460
Schechter, R.S.; Isbin, H.S.: Natural-convection heat transfer in regions of maximum fluid density. A.I.Ch.E. Jl4 (1958) 81–87
Vanier, C.R.; Tien, C.: Effect of maximum density and melting on natural convection heat transfer from a vertical plate. Chem. Engng. Prog. Sym. Ser.64 (1968) 240–254
Vanier, C.R.; Tien, C: Free convection melting of ice spheres. A.I.Ch.E. J116 (1970) 76–82
Bendell, M.: Gebhart, B.: Heat transfer and icemelting in ambient water near its density extremum. Int. J. Heat Transfer19 (1976) 1081–1087
Watson, A.: The effect of the inversion temperature on the convection of water in an enclosed rectangular cavity. Quart. J. Mech. Appl. Math.15 (1972) 423–446
Fujii, T.; Fujii, M.: On Grashof number in natural convection of water with density inversion. Preprints of 11th Japan Heat Transfer Symposium, C101 (1974) 369–372
Gosman, A.D.; Pun, W.M.; Runchal, A.K.; Spalding, D.B.; Wolfstein, M.: Heat and Mass Transfer.in Recirculating Flows. London-New York: Academic Press 1969
Hennecke, D.K.; Sparrow, E.M.; Ecker, E.R.G. Flow and heat transfer in a rotating enclosure with axial through flow. WÄrme- und Stoffübertragung4 (1971) 222–235
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Seki, N., Fukusako, S. & Inaba, H. Free convective heat transfer with density inversion in a confined rectangular vessel. Wärme- und Stoffübertragung 11, 145–156 (1978). https://doi.org/10.1007/BF01805655
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01805655