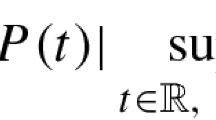Skip to main content
SpringerLink
Log in

A family of extension operators

  • Published:
Mathematical notes of the Academy of Sciences of the USSR Aims and scope Submit manuscript

Abstract

The definition of the degree of a family of extension operators is given. The connection of lower estimates with general properties is established. The problem of approximation of the segment [0, 1] by finite subsets is studied. In the class of homogeneous operators the independence of norms of operators from the degree of the family of extension operators is proved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature cited

  1. L. Collatz, Functional Analysis and Numerical Mathematics, Academic Press (1966).

  2. N. Bourbaki, Integration, Addison-Wesley.

  3. S. N. Bernshtein, Collected Works [in Russian], Vol. 2, Izd. Akad. Nauk SSSR, Moscow (1954).

    Google Scholar 

  4. S. K. Godunov, “A difference method for numerical computation of discontinuous solutions of equations of hydrodynamics,” Mat. Sb.,47, No. 3, 271–306 (1959).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Applied Mathematics, Academy of Sciences, USSR

    V. V. Pospelov

Authors
  1. V. V. Pospelov
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematicheskie Zametki, Vol. 22, No. 2, pp. 215–219, August, 1977.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pospelov, V.V. A family of extension operators. Mathematical Notes of the Academy of Sciences of the USSR 22, 610–613 (1977). https://doi.org/10.1007/BF01780969

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01780969

Keywords

Search

Navigation