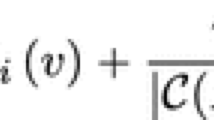Abstract
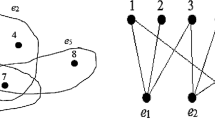
A communication situation consists of a game and a communication graph. By introducing two different types of corresponding communication games, point games and arc games, the Myerson value and the position value of a communication situation were introduced.
This paper investigates relations between convexity of the underlying game and the two communication games. In particular, assuming the underlying game to be convex, necessary and sufficient conditions on the communication graph are provided such that the communication games are convex. Moreover, under the same conditions, it is shown that the Myerson value and the posi tion value are in the core of the point game. Some remarks are made on superadditivity and balancedness.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Borm PEM, Owen G, Tijs S (1990) Values of points and arcs in communication situations. Report 9004, Dept of Mathematics, University of Nijmegen, The Netherlands
Myerson RB (1977) Graphs and cooperation in games. Math Oper Res 2, 225–229
Owen G (1986) Values of graph-restricted games. SIAM J Alg Disc Meth 7, 210–220
Shapley LS (1953) A value for n-person games. Annals of Math Studies 28, 307–317
Shapley LS (1971) Cores of convex games. Int J of Game Theory 1, 11–26
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
van den Nouweland, A., Borm, P. On the convexity of communication games. Int J Game Theory 19, 421–430 (1991). https://doi.org/10.1007/BF01766431
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01766431