Abstract
This article presents the formal analysis of a problem of the optimal flood control in systems of serially connected multiple water reservoirs. It is assumed, that the basic goal is minimization of the peak flow measured at a point (cross-section) located downstream from all reservoirs and that inflows to the system are deterministic. A theorem expressing sufficient conditions of optimality for combinations of releases from the reservoirs is presented together with the relevant proof. The main features of the optimal combinations of controls are thoroughly explained. Afterwards, two methods of determining the optimal releases are presented. Finally, the results of the application of the proposed methodology to a small, four reservoir system are presented.
Similar content being viewed by others
Abbreviations
- c i :
-
contribution of theith,i=1, ...,m, reservoir to the total storage capacity of the multireservoir system
- d i (t):
-
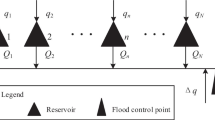
one of the uncontrolled inflows to the cascade at timet (fori=1 main inflow to the cascade, fori=2, ...,m, side inflow to theith reservoir, fori=m+1 side inflow at pointP)
- \(d_{s_i } (t)\) :
-
total inflow to theith reservoir,i=2, ...,m, at timet (i.e., inflowd i augmented with properly delayed releaser i−1 from the previous reservoir) (used only in figures)
- dΣ(t),d S (t):
-
(the first term is used in text, the second one in figures) aggregated inflow to the cascade (natural flow at pointP) at timet
- \(\dot d_\Sigma (t)\) :
-
time derivative of the aggregated inflow at timet
- i :
-
reservoir index
- m :
-
number of reservoirs in cascade
- P :
-
control point, flood damage center
- \(\bar q\) :
-
minimal peak of the flow at pointP (cutting level)
- Q p (t):
-
flow measured at pointP at timet
- \(\hat Q_p (t)\) :
-
flow measured at pointP at timet, corresponding to the optimal control of the cascade
- r i (t):
-
release from theith reservoir at timet, i=1, ...,m
- \(\hat r_i (t)\) :
-
optimal release from theith reservoir at timet, i=1, ...,m
- r * 1 (t):
-
a certain release from theith reservoir at timet, different than\(\hat r_i\),i=1, ...,m, (used only in the proof of Theorem 1)
- \(\tilde r_m (t)\) :
-
a piece of the optimal release from themth reservoir outside period\([t_a - t_{l_m } ,t_b - t_{l_m } ]\) at timet
- \(s_{a_i }\) :
-
assumed storage of theith reservoir at time\(s_{a_i }\) (used only in the proof of Theorem 1)
- s i (t):
-
storage of theith reservoir at timet, i=1, ...,m
- \(\dot s_i (t)\) :
-
time derivative of the storage of theith reservoir at timet, i=1, ...,m
- \(s_{i_{\max } }\) :
-
storage capacity of theith reservoir,i=1, ...,m
- \(s_{\Sigma _{\max } } ,s_{S_{\max } }\) :
-
(the first term is used in text, the second one in figures) total storage capacity of the cascade of reservoirs
- S*:
-
sum of storages, caused by implementingr * i ,i=1, ...,m, of all reservoirs measured at\(t_{b_i }\) (used only in the proof of Theorem 1)
- t :
-
time variable (continuous)
- t 0 :
-
initial time of the control horizon
- t a :
-
initial time of the period of constant flow equal\(\bar q\) at pointP
- \(s_{a_i }\) :
-
initial time of the period of the essential filling of theith reservoir,i=1, ...,m (used only in the proof of Theorem 1)
- t b :
-
final time of the period of constant flow equal\(\bar q\) at pointP
- \(t_{b_i }\) :
-
final time of the period of the essential filling of theith reservoir,i=1, ...,m (used only in the proof of Theorem 1)
- \(t'_{b_i }\) :
-
time of filling up of theith reservoir while applying method with switching of the active reservoir
- t f :
-
final time of the control horizon
- \(t_{l_i }\) :
-
fori=1, ...,m−1, time lag betweenith andi+1th reservoir; fori=m time lag between the lowest reservoir of the cascade and the control pointP
References
Dantzig, G. B. and Wolfe, P., 1960, Decomposition principle for linear programs,Operations Res. 8(1), 101–111.
Fiedorenko, R. P., 1978,Priblizhennoje reshenije zadach optimalnogo upravlenija, Nauka, Moscow.
Karbowski, A., 1989, Synthesis of structures and mechanisms of flood control in multireservoir systems, Ph.D. Thesis, Warsaw University of Technology, Warsaw.
Karbowski, A., 1991, Optimal control of single retention reservoir during flood; Solution of deterministic, continuous-time problems,J. Optim. Theory Appl. 69(1), 55–81.
Loaiciga, H. A. and Mariño, M. A., 1985, An approach to parameter estimation and stochastic control in water resources with an application to reservoir control,Water Resour. Res. 21(11), 1575–1584.
Mariën, J. L., 1981, Real-time operation of a cascade of flood reservoirs in small river basins, in T. E. Unny and E. A. McBean (eds.),Proceedings of the International Symposium on Real-Time Operation of Hydrosystems, Waterloo, Waterloo University Press, Waterloo, Ontario, Canada, pp. 354–368.
Mariën, J. L., 1984, Controllability conditions for reservoir flood control systems with applications,Water Resour. Res. 20(11), 1477–1488.
Oberle, H. J., 1986, Numerical solution of minimax optimal control problems by multiple shooting technique,J. Optim. Theory Appl. 50(2), 331–357.
Pytlak, R. and Malinowski, K., 1989, Optimal scheduling of reservoir releases during flood: deterministic optimization problem, Part I and Part II,J. Optim. Theory Appl. 61(3), 409–432 and 433–449.
Unver, O. I. and Mays, L. W., 1990, Model for real-time optimal flood contol operation of a reservoir system,Water Resour. Manage. 4, 21–26.
Wasimi, S. A. and Kitanidis, P. K., 1983, Real-time forecasting and daily operation of a multireservoir system during floods by linar quadratic Gaussian control,Water Resour. Res. 19(6), 1511–1521.
Windsor, J. S., 1973, Optimization models for the operation of flood control systems,Water Resour. Res. 9(5), 1219–1226.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Karbowski, A. Optimal flood control in multireservoir cascade systems with deterministic inflow forecasts. Water Resour Manage 7, 207–223 (1993). https://doi.org/10.1007/BF01675304
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01675304