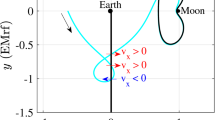
Abstract
Analytical techniques are employed to demonstrate certain invariant properties of families of moon-to-earth trajectories. The analytical expressions which demonstrate these properties have been derived from an earlier analytical solution of the restricted three-body problem which was developed by the method of matched asymptotic expansions. These expressions are given explicitly to orderµ 1/2 where μ is the dimensionless mass of the moon. It is also shown that the inclusion of higher order corrections does not affect the nature of the invariant properties but only increases the accuracy of the analytic expressions.
The results are compared with the work of Hoelker, Braud, and Herring who first discovered invariant properties of earth-to-moon trajectories by exact numerical integration of the equations of motion. (Similar properties for moon-to-earth trajectories follow from the principle of reflection). In each instance the analytical expressions result in properties which are equivalent, to orderµ 1/2, with those found by numerical integration. Some quantitative comparisons are presented which show the analytical expressions to be quite accurate for calculating particular geometrical characteristics.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Abbreviations
- \(\bar h\) :
-
energy
- \(\bar l\) :
-
angular momentum
- ā :
-
semi-major axis
- \(\bar \varepsilon \) :
-
eccentricity
- ī :
-
inclination
- \(\bar \Omega \) :
-
argument of node
- \(\bar \theta \) :
-
argument of pericynthion
- h e :
-
energy
- l e :
-
angular momentum
- i :
-
inclination
- Ω:
-
argument of node
- ω:
-
argument of perigee
- t f :
-
time of flight
- \(\bar k,\bar m,\bar n,\bar b,\bar c,\bar d\) :
-
parameters used in matehing
- U :
-
a function of the energy near the earth
- λ:
-
a function of the angular momentum near the earth
- r p :
-
perigee radius
- \(\bar r_p \) :
-
perincynthion radius
- \(\bar r_n \) :
-
radius at node near moon
- \(\bar v_n \) :
-
true anomaly of node near moon
- \(\bar \sigma ^* \) :
-
initial angle between node near moon and earth-moon line
- \(\bar H\) :
-
a function ofU, λ,\(\bar r_p \) andi
- ϕ:
-
earth phase angle
- μ:
-
dimensionless mass of the moon
- U 0, U1 :
-
U=U 0+μU 1
- i 0, i1/2, i1 :
-
i=i 0+µ 1/2 i 1/2+µ i 1
- ω 0,ω 1/2,ω 1 :
-
ω=ω 0+µ 1/2 i 1/2+µ i 1
- ψ p :
-
longitude of vertex line
- ψ n :
-
latitude of vertex line
- R o ,S o ,N o :
-
functions ofU 0 and λ
- \(\bar R_o \) :
-
a function ofU 0,ī and\(\bar r_p \)
References
Herring, G. P.: 1964, ‘A Comprehensive Astrodynamic Exposition and Classification of Earth-Moon Transits’, NASA TM X-53151.
Hoelker, R. F. and Braud, N. J.: 1963 ‘Survey and Classification of Earth-Moon Trajectories Based on Newly Discovered Properties’, AIAA Paper 63-150.
Hoelker, R. F. and Braud, N. J.: 1964, ‘Mapping a Course for the Moon Trip’,Astronaut. Aeron. 16–23.
Lagerstrom, P. A. and Kevorkian, J.: 1963, ‘Earth-to-Moon Trajectories in the Restricted Three-Body Problem’,J. Mecan. 2, 189–218.
Lagerstrom, P. A. and Kevorkian, J.: 1966, ‘Nonplanar Earth-to-Moon Trajectories in the Restricted Three-Body Problem’,AIAA J. 4, 149–152.
Lancaster, J. E. and Kevorkian, J.: 1968, ‘Nonplanar Moon-to-Earth Trajectories’,AIAA J. 6, 1986–1991.
Lancaster, J. E., Walker, J. C., and Mann, F. I.: 1969, ‘Rapid Analysis of Moon-to-Earth Trajectories’,AIAA J. 7, 1017–1023.
Lancaster, J. E.: 1970, ‘Numerical Analysis of the Asymptotic Solution for Two-Point Boundary Value Moon-to-Earth Trajectories’, to be presented to the AAS/AIAA Astrodynamics Specialist Conference, Santa Barbara, California, August 19–21, 1970.
Szebehely, V.: 1967,Theory of Orbits, Academic Press, New York, pp. 579–582.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Lancaster, J.E. Invariant properties of families of moon-to-earth trajectories. Celestial Mechanics 2, 481–493 (1970). https://doi.org/10.1007/BF01625280
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01625280