Farey nets and multidimensional continued fractions

Abstract

A multidimensional continued fraction algorithm is a generalization of the ordinary continued fraction algorithm which approximates a vector η=(y ₁,...,y _n ) by a sequence of vectors$\left( {\frac{{a_{j,1} }}{{a_{j,n + 1} }}, \ldots ,\frac{{a_{j,n} }}{{a_{j,n + 1} }}} \right)$. If 1,y ₁,...,y _n are linearly independent over the rationals, then we say that the expansion of η isstrongly convergent if

$$\mathop {\lim }\limits_{j \to \infty } \left| {\left( {\frac{{a_{j,1} }}{{a_{j,n + 1} }}, \ldots ,\frac{{a_{j,n} }}{{a_{j,n + 1} }}} \right) - \eta } \right| = 0.$$

This means that the algorithm converges at an asymptotically faster rate than would be guaranteed just by picking a denominator at random.

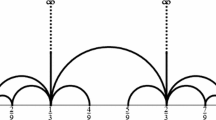
The ordinary continued fraction algorithm can be defined using the Farey sequence, approximating a number by the endpoints of intervals which contain it. Analogously, we can define a Farey netF _{n, m} to be a triangulation of the set of all vectors$\left( {\frac{{a_1 }}{{a_{n + 1} }}, \ldots ,\frac{{a_n }}{{a_{n + 1} }}} \right)$ witha _n+1 ≤m into simplices of determinant ±1, and use this algorithm to define a multidimensional continued fraction for η in which the approximations are the vertices of the simplices containing η in a sequence of Farey nets. The concept of a Farey net was proposed by A. Hurwitz, and R. Mönkemeyer developed a specific continued fraction algorithm based on it.

We show that Mönkemeyer's algorithm discovers dependencies among the coordinates of η in two dimensions, but that no continued fraction algorithm based on Farey nets can discover dependencies in three or more dimensions, and none can be strongly convergent, even in two dimensions. Thus there are no good multidimensional algorithms based on Farey nets.