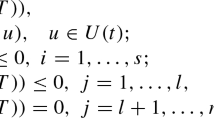Pontryagin's maximum principle for a constrained system of ordinary differential equations

Summary

Recently TIMMAN [2] succeeded in setting up a theory of optimization by applying variational principles to problems of mathematical programming and control theory. These principles may be considered as basic when dealing with problems of optimization theory. In this paper we are concerned with a general problem of control theory: inequality-constraints for both the control-variables and the state-variables are taken into account. The point is to derive necessary conditions for the optimal control, which is such that the solution of a set of ordinary differential equations minimizes some given integral. Moreover end-conditions will be considered.