Skip to main content
SpringerLink
Log in

An approximate calculation of the stress and deformation concentrations in the plastic region and during creep

  • Scientific-Technical Section
  • Published:
Strength of Materials Aims and scope

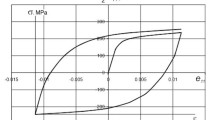
Conclusions

  1. 1.

    In the normal distribution the arithmetic mean is the most probable value of the exact or true quantity [19, 20]. Therefore calculations of the maximum stresses and deformations based on Eqs. (1) and (2) lead to nearly accurate results, because their arithmetic mean errors are practically zero.

  2. 2.

    There are no experimental data on the stress and deformation concentrations in the plastic region and during creep for circular solid and hollow shafts with an annular notch or fillet. Therefore we cannot find the error in determining the theoretical values of the maximum stresses and deformations. Comparison with the results of other different approximate solutions, including the method of finite elements [21], shows that the error in determining the stresses does not exceed ±10%.

  3. 3.

    For calculation by Eqs. (1) and (2) we need a deformation curve and the modulus of elasticity of the material (or the isochronic creep curves), the theoretical stress concentration coefficient, and the nominal stress in the theoretical cross section.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature Cited

  1. H. F. Hardrath and L. Ohman, “A study of elastic and plastic stress concentration factors due to notches and fillets in flat plates,” NACA TN, No. 2566 (1951).

  2. H. Neiber, “The theory of stress concentration in prismatic rods under shear for any nonlinear law relating stress to deformation,” in: Symposium of Translations “Mekhanika,” No. 4 (1961).

  3. E. Z. Stowell, “Stress and strain concentration at a circular hole in an infinite plate,” NACA TN, No. 2073 (1950).

  4. J. Javornicky, “Plastic stress and strain concentration factors in a strip with a hole of notches under tension,” The Journ. of Strain Analysis,3, No. 1 (1968).

  5. B. M. Wundt, Effect of Notches on Low-Cycle Fatigue. A Literature Survey. ASTM. Special Technical Publication, 490, Philadelphia (1972).

  6. A. Thum and W. Buchmann, “Kerbempfindlichkeit von Stälen,” Archiv für das Eisenhüttenwessen,7, No. 11 (1934).

  7. Ch. G. Mustafin, “On the stress and deformation concentration in the plastic region and during creep,” Mashinovedenie, No. 3 (1975).

  8. N. A. Borodin and S. V. Serensen, “On long-term static failure in the concentration zone,” Izv. Akad. Nauk SSSR, Otd. Tekh. Nauk, Mekhanika i Mashinostroenie, No. 4 (1960).

  9. I. I. Bugakov, V. P. Smirnova and S. P. Shikhobalov, “Modeling the creep of a T-shaped shaft of a turbine blade,” in: Investigations on Elasticity and Plasticity [in Russian], No. 3, Izd. LGU, Leningrad (1964).

    Google Scholar 

  10. G. Kostov, “Determination of the stress concentration factor in the plastic region under static load,” Tekhnicheska Mis'l,5 No. 3 (1968).

  11. I. I. Faerberg, “Tension of a plate with a circular hole at the elastic limit,” in: Trudy TsAGI, No. 615. BNT, Moscow (1947).

    Google Scholar 

  12. W. A. Box, “The effect of plastic strains on stress concentrators,” Proc. of the SESA,8, No. 2 (1951).

  13. M. Kh. Akhmetzyanov, “Investigation of stress concentration in the plastic region by means of photoelastic coatings,” Izv. Akad. Nauk SSSR, Otd. Tekh. Nauk, Mekhanika i Mashinostroenie, No. 1 (1963).

  14. A. Durelli and Z. Sciamarella, “Distribution of elastoplastic stresses and deformations in a uniformly streteched plate with a hole,” Applied Mechanics, Proceedings of American Society of Mechanical Engineers [Russian translation], Vol. 30, No. 2 (1963).

  15. P. S. Theocaris and E. Marcetos, “Elastic-plastic analysis of perforated thin strips of a strain hardening material,” Journ. of the Mech. and Phys. of Sol.,12, No. 6 (1964).

  16. N. V. Smirnov and I. V. Dunin-Barkovskii, Course in the Theory of Probability and Mathematical Statistics for Technical Applications [in Russian], Nauka, Moscow (1965).

    Google Scholar 

  17. R. B. Heywood, Designing by Photoelasticity, Chapman and Hall Ltd., London (1952).

    Google Scholar 

  18. Yu. N. Rabotnov, Creep in Structural Elements [in Russian], Nauka, Moscow (1966).

    Google Scholar 

  19. K. P. Yakovlev, Mathematical Processing of the Results of Measurements [in Russian], Gostekhizdat, Moscow (1953).

    Google Scholar 

  20. H. Schenck, Theories of Engineering Experimentation, McGraw-Hill (1968).

  21. D. F. Mowbray and J. E. McConnelee, “Application of finite element elastic-plastic stress analysis to notched fatigue specimen behavior,” Proceedings of the First International Conference on Structural Mechanics in Reactor Technology, Berlin, Germany, September, 1971, Vol. 6, Pt. M, Berlin (1972), pp. 20–25.

    Google Scholar 

Download references

Authors
  1. Ch. G. Mustafin
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Leningrad. Translated from Problemy Prochnosti, No. 5, pp. 78–81, May, 1976.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mustafin, C.G. An approximate calculation of the stress and deformation concentrations in the plastic region and during creep. Strength Mater 8, 581–585 (1976). https://doi.org/10.1007/BF01528618

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01528618

Keywords

Search

Navigation