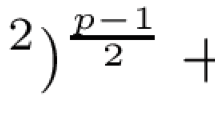Abstract
For the bilinear forma(u, v) = ∫ Ω a ij (x)u xi v xj dx, whereu, v∈H 10 (Ω), Ω a bounded domain in ℝn, anda ij (x) bounded and uniformly elliptic coefficients on Ω, theL p integrability on Ω forp>2n/(n−2) of the solution to the variational inequality (the unilateral obstacle problem with obstacle
is studied. Hereψ is an arbitrary function given on Ω andC is the Newtonian conductor capacity relative to Ω. The sufficient conditions that permit such quantitative estimates are given in terms of capacitary integrals on Ω:∫|ψ| q dC<∞. Some simple examples show that is not sufficient to assume merely thatψ∈H 10 (Ω)∩L q(Ω) for sufficiently largeq. In particular,\(\mathbb{K}_\psi \ne \emptyset \) precisely when∫ψ 2+ dC<∞. An estimate is also given for theL p norm of the gradient of such solutions in terms of these integrals.
Similar content being viewed by others
References
D. R. Adams,L p-capacitary integrals with some applications,Proc. Symp. Pure Math., AMS, 35, 359–367 (1979).
D. R. Adams, Sets and functions of finiteL p-capacity,Ind. U. Math. J., 27, 611–627 (1978).
D. R. Adams, The existence of capacitary strong type estimates inR n,Ark. för Math., 14, 125–140 (1976).
D. R. Adams, A note on Riesz potentials,Duke Math. J., 42, 765–778 (1975).
L. Boccardo, RegulariteW 1,p0 (2<p<∞) de la solution d'un probleme unilateral (unpublished).
H. Brezis, Problemes unilateraux,J. Math. Pures Appl., 51, 1–168 (1972).
L. Cafferarelli and D. Kinderlehrer, Potential methods in variational inequalities,J. D'Anal. Math., 37, 285–295 (1980).
G. Choquet, Theory of capacities,Ann. Inst. Fourier, 5, 131–295 (1953).
D. Kinderlehrer and G. Stampacchia,An Introduction to Variational Inequalities and Their Applications, Academic Press, New York 1980.
H. Lewy, and G. Stampacchia, On the regularity of the solution of a variational inequality,Comm. Pure Appl. Math., 22, 153–188 (1969).
V. G. Maz'ya, Imbedding theorems and their applications, Baku Symp. (1966), “Nauk” Moscow, 141–159 (1970). (Russian).
V. G. Maz'ya, On some integral inequalities for functions of several variables,Problems in Math. Analysis, No. 3 (1972), Leningrad U. (Russian).
G. Stampacchia, Le probleme de Dirichlet pour les equations elliptique du second order à coefficients discontinuous,Ann. Inst. Fourier (Grenoble), 15, 189–258 (1965).
E. M. Stein,Singular Integrals and Differentiability Properties of Functions, Princeton U. Press, Princeton 1970.
Author information
Authors and Affiliations
Additional information
Communicated by D. Kinderlehrer
This work was partially supported by National Science Foundation grant MCS 80-02840.
Rights and permissions
About this article
Cite this article
Adams, D.R. Capacity and the obstacle problem. Appl Math Optim 8, 39–57 (1982). https://doi.org/10.1007/BF01447750
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01447750