Skip to main content
SpringerLink
Log in

A geometric property of Hill's curves

  • Published:
Celestial mechanics Aims and scope Submit manuscript

Abstract

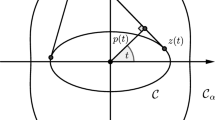
The following is proved in this note: If we construct a circle passing through a given primary in the planar circular restricted three-body problem, center of which is the remaining primary, then the minor arc of this circle with endpoints represented by the triangular libration points represents-when the given primary is excluded-locus of all the points on the Hill's curves that are the least distant points from the given primary.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Reference

  • Moulton, F. R.: 1902,An Introduction to Celestial Mechanics, The Macmillan Company, New York, Macmillan & Co., Ltd., London.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Astronomical Institute, Czechoslovak Academy of Sciences, Budečská 6, Vinohrady, 120 23, Praha 2, Czechoslovakia

    Vladimír Matas

Authors
  1. Vladimír Matas
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Matas, V. A geometric property of Hill's curves. Celestial Mechanics 17, 193–194 (1978). https://doi.org/10.1007/BF01371330

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01371330

Keywords

Search

Navigation