Abstract
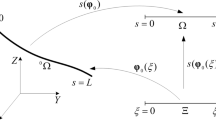
The minimum weight problem of a shallow circular beam is studied in the case when the beam has a piece-wise constant thickness. The minimum of the weight is sought under the condition that the deflections of the beam of piece-wise constant thickness do not exceed those of the reference beam of constant thickness for given values of the external loading. The beam is subjected to uniformly distributed transverse pressure and to axial dead load. The material of the beam is assumed to be ideally rigid-plastic. Moderately large deflections are taken into account. Necessary optimality conditions are derived and used in order to establish the optimal values of the design parameters.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bryson, A.E.; Ho, Y.C. 1969:Applied optimal control. Blaisdell: Waltham
Foulkes, J. 1953: Minimum weight design and the theory of plastic collapse.Q. Appl. Math. 10, 347–358
Foulkes, J. 1954: The minimum weight design of structural frames.Proc. Roy. Soc. A 223, 482–494
Hopkins, H.G.; Prager, W. 1955: Limits of economy of material in plates.J. Appl. Mech. 22, 372–374
Kondo, K.; Pian, T.H.H. 1981: Large deformations of rigid-plastic beams.J. Struct. Mech. 9, 139–159
Kreindler, E. 1982: Additional necessary conditions for optimal control with state-variable inequality constraints.J. Optimiz. Theory Appl. 38, 241–250
Lamblin, D.O.; Guerlement, G.; Save, M.A. 1985: Solutions de dimensionnement plastique de volume minimal de plaques circulaires pleines et sandwiches en presence de contraintes technologiques.J. Mech. Theor. Appl. 4, 433–461
Lellep, J. 1991:Optimization of plastic structures. Tartu: Tartu University Press
Lellep, J.; Hein, H. 1993: Optimization of rigid-plastic shallow spherical shells of piece-wise constant thickness.Struct. Optim. 6, 134–141
Lellep, J.; Hein, H. 1994: Optimization of clamped rigid-plastic shallow shells of piece-wise constant thickness.Int. J. Non-Linear Mech. 29, 625–636
Lellep, J.; Majak, J. 1985: Optimal design of plastic beams with piece-wise constant thickness (in Russian).Tartu Ülik. 721, 16–24
Lellep, J.; Majak, J. 1993: Optimal design of plastic annular plates of von Mises material in the range of large deflections.Struct. Optim. 5, 197–203
Massonet, C.; Save, M. 1965: Beams and frames (plastic analysis and design). New York: Blaisdell
Rozvany, G.I.N. 1976:Optimal design of flexural systems. Oxford: Pergamon
Sheu, C.Y.; Prager, W. 1969: Optimal plastic design of circular and annular sandwich plates with piece-wise constant cross-section.J. Mech. Phys. Solids 17, 11–16
Speyer, J.L.; Bryson, A.E. 1968: Optimal programming problems with a bounded state space.AIAA J. 6, 1488–1491
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Lellep, J., Hein, H. Optimization of rigid-plastic shallow curved beams. Structural Optimization 12, 57–62 (1996). https://doi.org/10.1007/BF01270444
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01270444