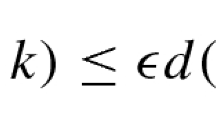Abstract
IfM is a closed Nil geometry 3-manifold then π1(M) is almost convex with respect to a fairly simple “geometric” generating set. IfG is a central extension or a ℤ extension of a word hyperbolic group, thenG is also almost convex with respect to some generating set. Combining these with previously known results shows that ifM is a closed 3-manifold with one of Thurston's eight geometries, π1(M) is almost convex with respect to some generating set if and only if the geometry in question is not Sol.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Cannon, J.: Almost convex groups,Geom. Dedicata 22 (1987), 197–210.
Cannon, J., Floyd, W., Grayson, M. and Thurston, T.: Solvgroups are not almost convex,Geom. Dedicata 31 (1989), 291–300.
Scott, P.: The Geometries of three-manifolds,Bull. London Math. Soc. 15 (1983), 401–487.
Shapiro, M.: A Geometric approach to the almost convexity and growth of some nilpotent groups,Math. Ann. 285 (1989), 601–624.
Shapiro, M.: Growth of a\(P\widetilde{SL_2 }\mathbb{R}\) manifold group (to appear inMathematische Nachrichten).
Short, H. (ed.): Notes on word hyperbolic groups, in E. Ghys, A. Haefliger and A. Verjovsky (eds), Group Theory from a Geometric Viewpoint, World Scientific.
Thiel, C.: Zur Fast-Konvexität einiger nilpotenter Gruppen,Bonner Math. Schriften, 1992.