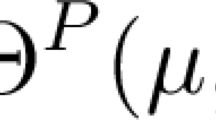Abstract
It is well known that isolated singularities of two dimensional analytic vector fields can be desingularized: after a finite number of blowing up operations we obtain a vector field that exhibits only elementary singularities. In the present paper we introduce a similar method to simplify the periodic limit sets of analytic families of vector fields. Although the method is applied here only to reduce to families in which the zero set has codimension at least two, we conjecture that it can be used in general. This is related to the famouss Hibert's problem about planar vector fields.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
[BJ]Bröcker Th., Janich K., Introduction to Differential Topology, Cambridge Unviersity Press, 1973.
[BM]Bierstone E., Milman P., Semianalytic and subanalytic sets, IHES, Publications Math. nr 67, p. 1–42, 1988.
[B]Bogdanov R., Versal deformations of a singular point of a vector field on the plane in the case of zero eigenvalues, Seminaria Petrovsky 1976, Sel. Math. Sov. 1 (4) 1981.
[D1]Dumortier F., Singularities of vector fields on the plane, J. Diff. Equations, 23, 2, (1977) 53–166.
[D2]Dumortier, F., Singularities of vector fields, publ. IMPA, (1978)..
[DR1]Dumortier F., Roussarie R., Tracking limit cycles escaping from rescaling domains (to appear).
[DR2]Dumortier F. Roussarie R., Duck cycles and central manifolds (to appear).
[DRS1]Dumortier F., Roussarie R., Sotomayor J., Generic 3-parameter families of vector fields on the plane, unfolding a singularity with nilpotent linear part. The cusp case of codimension 3. Erg. Th. and Dyn. Syst. vol. 7, p. 375–413, 1987.
[DRS2]Dumortier F., Roussarie R., Sotomayor J., Generic 3-parameter families of planar vector fields, unfoldings of saddle, focus and elliptic singularites with nilpotent linear part. Lect. Notes of Maths., 1480, 1991.
[DRS3]Dumortier, F., Roussarie R., Sotomayor J., Bifurcations of cuspidal loops (to appear).
[FP]Françoise J. P., Pugh C. C., Keeping track of limit cycles. J. Diff. Eq. 64, (1986) 139–157.
[H]Hervé H., Several complex Variables, Oxford University Press, 1963.
[K]Kuratowski K., Topology, vol. 2, Academic Press, N.Y. London, 1966.
[R1]Roussarie R., Note on the Finite cyclicity property and Hilbert's 16th problem, Lect. Notes in Math. no. 1331, Dynamical Systems-Valparaiso 1986, R. Bamon, R. Labarca, J. Palis ed. (1988).
[R2]Roussarie R., Cyclicité finie des lacets et des points cuspidaux. Nonlinearity 2, 73–117, 1989.
[R3]Roussarie R., Desingularization of unfoldings of cusp loops, preprint, 1989, to appear in Acta of “Workshop: Chaotic dynamics and bifurcations”, march 1989, H. Broer and F. Takens org.
[R4]Roussarie R., Desingularization of analytic families of planar vector fields without singular points of vanishing linear part, to appear.
[S]Seidenberg A., Reduction of singularities of the equationAdy=Bdx, Amer, J. Math., (1968) 248–269.
[Ta]Takens F., Forced oscillations and bifurcations. In Applications of Global Analysis I, Communications of Math. Inst. Rijksuniversitat, Utrecht 3, 1974.
[T]Tougeron J. Cl., Ideaux de fonctions différentiables, Springer Verlag 1972.
[Tr]Trifonov S. I., Desingularisation of singularities in families of analytic differential equations (Preprint in Russian).
[V]Van den Essen, Reduction of singularities of the equationAdy=Bdx, L. N. M. 712, 1979, p. 44–60.
Author information
Authors and Affiliations
About this article
Cite this article
Denkowska, Z., Roussarie, R. A method of desingularization for analytic two-dimensional vector field families. Bol. Soc. Bras. Mat 22, 93–126 (1991). https://doi.org/10.1007/BF01244900
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01244900