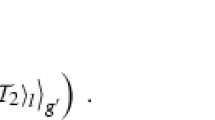Satellites and Riemannian geometry

Abstract

In an axially symmetric three-dimensional Riemann-spaceg _ik(u ¹,u ²)−u ³ represents the cyclic parameter-, a gravitational potential ϕ(u ¹,u ²) is given. For all masspoints with equal total energy and equal angular momentum there exists a function Ψ(u ¹,u ²) by means of which the equations of motion can be reduced to a simple ordinary second-order differential equation. The function ϕ can be interpreted as the velocity with which the masspoint moves in the two-dimensional spaceu ¹,u ².

Of particular interest is the case where the spaceu ¹,u ²,u ³ is Euclidean. Ifu ¹,u ² are Cartesian coordinates in a planeu ³=const., and if the tangent vector of the trajectoryu ¹(t)u ²(t) has the components cosω, sinω it is shown that the triple integral

$$\smallint \smallint \smallint \psi du^1 du^2 d\omega $$

is an invariant integral in Cartan's sense, in other words, if the integral is extended over a domain in a meridian plane at timet=0, it keeps its value at any time.