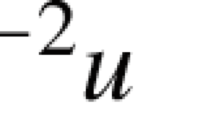Abstract
The integral operator which sends f (ζ) into
x and ζ ∈ RP, is shown to map the space of functions f (ζ) on |ζ|<1, square integrable with respect to the weight (1-|ξ|2)1/2 one to one onto the space of functions g (x) on |x|<1 which possess gradients δg(x) in the sense of distribution theory, with both g(x) and δg(x) being square integrable with respect to the weight (1-|x|2)1/2. This extends to p≥3 a result of P. Wolfe's in the case p=2.
Similar content being viewed by others
References
Erdelyi, A.: Higher Transcendental Functions, Vol. I, New York, McGraw-Hill Book Company, Inc. 1953.
Hobson, E. W.: The Theory of Spherical and Ellipsoidal Harmonics, New York, Chelsea Publishing Company, 1955.
Kahane, C. S.: The solution of a mildly singular integral equation of the first kind on a disk, Integral Equations and Operator Theory, Vol. 4 (1981), 548–595.
Kahane, C. S.: The solution of a mildly singular integral equation on a ball, To appear in Integral Equations and Operator Theory.
Mikhlin, S. G.: Mathematical Physics, an Advanced Course (Translated from the Russian), Amsterdam, North-Holland Publishing Company 1970.
Necas, J.: Les Méthodes Directes en Théorie des Équations Elliptiques, Paris, Masson 1967.
Vilenkin, N. Ja.: Special Functions and the Theory of Group Representations, Translations of Mathematical Monographs, Vol. 22, Providence, American Mäthematical Society 1968.
Wolfe, P.: Eigenfunctions of the integral equation for the potential of the charged disk, J. Math. Phys. 12 (1971), 1215–1218.
Wolfe, P.: An integral operator arising in potential theory, Applicable Anal. 10 (1980), 71–80.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kahane, C.S. Extension of a theorem of P. Wolfe on singular integral equations. Integr equ oper theory 7, 96–117 (1984). https://doi.org/10.1007/BF01204915
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01204915