Skip to main content
SpringerLink
Log in

Nilpotent and solvable radicals in locally finite congruence modular varieties

  • Published:
algebra universalis Aims and scope Submit manuscript

Abstract

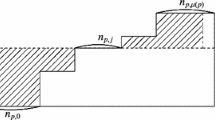
The Loewy rank of a modular latticeL of finite height is defined as the leastn for which there exista 0=0<at, < ... <ar=1 inL such that each interval I[ai, ai+1] is a complemented lattice. In this paper, a generalized notion of Loewy rank is applied to obtain new results in the commutator theory of locally finite congruence modular varieties. LetV be a finitely generated congruence modular variety. We prove that every algebra inV has a largest nilpotent congruence and a largest solvable congruence. Moreover, there exist first order formulas which define these special congruences in every algebra ofV.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. A. Baker Finite equational bases for finite algebras in a congruence-distributive equational class, Advances in Math.24 (1977), 207–243.

    Google Scholar 

  2. S.Burris and H. P.Sankappanavar. A COURSE IN UNIVERSAL ALGEBRA, Springer-Verlag, Graduate Texts in Mathematics v. 78.

  3. R. Freese andR. McKenzie Residually small varieties with modular congruence lattices, Trans. Amer. Math. Soc.264 (1981), 419–430.

    Google Scholar 

  4. R.Freese and R.McKenzie Commutator theory for congruence modular varieties, London Math. Soc. Lecture Note series, vol. 125, 1987.

  5. H. P. Gumm An easy way to the commutator in modular varieties, Archiv der Math. (Basel)34 (1980), 220–228.

    Google Scholar 

  6. H. P. Gumm Congruence modularity is permutability composed with distributivity, Archiv der Math. (Basel)36 (1981), 569–576.

    Google Scholar 

  7. H. P.Gumm Geometrical methods in congruence modular algebras, Memoirs of the Amer. Math. Soc.286 (1983).

  8. J. Hagemann andC. Herrmann A concrete ideal multiplication for algebraic systems and its relation to congruence distributivity, Archiv der Math. (Basel)32 (1979), 234–245.

    Google Scholar 

  9. D.Hobby and R.McKenzie The structure of finite algebras (Tame congruence theory), Amer. Math. Soc. Contemporary Mathematics series [to appear].

  10. A. Loewy Über reduzible lineare homogene Differentialgleichungen. Math. Ann.56 (1903), 549–584.

    Google Scholar 

  11. R. McKenzie Finite equational bases for congruence modular varieties, Algebra Universalis24 (1987), 224–250.

    Google Scholar 

  12. S. Oates-MacDonald andM. Vaughan-Lee Varieties that make one Cross. J. Austral. Math. Soc. (Series A)26 (1978), 368–82.

    Google Scholar 

  13. H. J. Zassenhaus THE THEORY OF GROUPS, Chelsea Publ. Co. (2nd Ed.), New York 1958.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of California at Berkeley, Berkeley, California, USA

    Ralph McKenzie

Authors
  1. Ralph McKenzie
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Research supported by National Science Foundation Grant No. DMS-8302295.

Rights and permissions

Reprints and permissions

About this article

Cite this article

McKenzie, R. Nilpotent and solvable radicals in locally finite congruence modular varieties. Algebra Universalis 24, 251–266 (1987). https://doi.org/10.1007/BF01195264

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01195264

Keywords

Search

Navigation