Summary
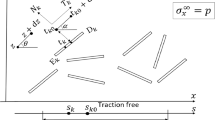
The interaction of time harmonic antiplane shear waves with nonplanar cracks embedded in an elastic half-space is studied. Based on the qualitatively similar features of crack and dislocation, with the aid of image method, the problem can be formulated in terms of a system of singular integral equations for the density functions and phase lags of vibrating screw dislocations. The integral equations, with the dominant singular part of Hadamard's type, can be solved by Galerkin's numerical scheme. Resonance vibrations of the layer between the cracks and the free surface are observed, which substantially give rise to high elevation of local stresses. The calculations show that near-field stresses due to scattering by a single crack and two cracks are quite different. The interaction between two cracks is discussed in detail. Furthermore, by assuming one of the crack tips to be nearly in contact with the free surface, the problem can be regarded as the diffraction of elastic waves by edge cracks. Numerical results are presented for the elastodynamic stress intensity factors as a function of the wave number, the incident angle, and the relative position of the cracks and the free surface.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Loeber, J. F., Sih, G. C.: Diffraction of antiplance shear waves by a finite crack. J. Acoust. Soc. Am.44, 90–98 (1968).
Jain, S. L., Lanwal, R. P.: Diffraction of elastic waves by two coplanar Griffith cracks in an infinite elastic medium. Int. J. Solids Struct.8, 961–975 (1972).
Itou, S.: Diffraction of an antiplane shear wave by two coplanar Griffith cracks in an infinite elastic medium. Int. J. Solids Struct.16, 1147–1153 (1980).
Datta, S. K.: Diffraction of SH-waves by an edge crack. J. Appl. Mech.46, 101–106 (1979).
Stone, S. F., Ghosh, M. L., Mal, A. K.: Diffraction of antiplane shear waves by an edge crack. J. Appl. Mech.47, 359–362 (1980).
Achenbach, J. D., Keer, L. M., Mendelsohn, D. A.: Elastodynamic analysis of an edge crack. J. Appl. Mech.47, 551–556 (1980).
Achenbach, J. D., Brind, R. J.: Elastodynamic stress intensity factors for a crack near a free surface. J. Appl. Mech.48, 539–542 (1981).
Keer, L. M., Lin, W., Achenbach, J. D.: Resonance effects for a crack near a free surface. J. Appl. Mech.51, 65–70 (1984).
Lin, W., Keer, L. M., Achenbach, J. D.: Dynamic stress intensity factors for an inclined subsurface crack. J. Appl. Mech.51, 773–779 (1984).
Shah, A. H., Wong, K. C., Datta, S. K.: Dynamic stress intensity factors for buried planar and nonplanar cracks. Int. J. Solids Struct.22, 845–857 (1986).
Shah, A. H., Chin, Y. F., Datta, S. K.: Elastic wave scattering by surface-bresking planar and nonplanar cracks. J. Appl. Mech.54, 761–767 (1987).
Abrahams, I. D., Wickham, G. R.: Scattering of elastic waves by an arbitrary small imperfection in the surface of a half-space. J. Mech. Phys. Solids40, 1683–1706 (1992).
Huang, J. Y., So, H.: Determination of dynamic stress intensity factor by dislocation model. Int. J. Fracture36, 187–198 (1988).
Huang, J. Y., So, H.: Diffraction of P waves by two cracks at arbitrary position in an elastic medium. Eng. Fract. Mech.29, 335–347 (1988).
So, H., Huang, J. Y.: Determination of dynamic stress intensity factors of two finite cracks at arbitrary positions by dislocation model. Int. J. Eng. Sci.26, 111–119 (1988).
Eshelby, J. D.: Dislocation as a cause of mechanical damping in metals. Proc. R. Soc. London Ser.A 197, 396–416 (1949).
Hirth, J. P., Lothe, J.: Theory of dislocation. New York: John Wiley 1982.
Achenbach, J. D.: Wave propagation in elastic solid. New York: North-Holland 1973.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Huang, J.Y. Elastodynamic analysis of nonplanar cracks in a half-space. Acta Mechanica 115, 67–78 (1996). https://doi.org/10.1007/BF01187429
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01187429