The problem of unphysical states in the theory of intermolecular interactions

Abstract

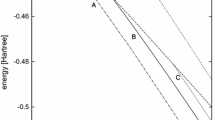
It was shown by Claverie that the interactions between atoms and molecules make unphysical electronic solutions of the Schradinger equation accessible in perturbation calculations of intermolecular interactions, accessible in the sense that the perturbation expansion is likely to converge to an unphysical solution if it converges at all. This is a difficult problem because there are generally an infinite number of unphysical states with energies below that of the physical ground state. We have carried out configuration interaction calculations on LiH of both physical and unphysical states. They show that avoided crossings occur between physical and unphysical energy levels as the interaction between the two atoms is turned on, i.e. as the expansion parameter λ is increased from 0 to 1. The avoided crossing for the lowest energy state occurs for λ < 0.8, implying that the perturbation expansion will diverge for larger values of λ. The behavior of the energy levels as functions of λ. is shown to be understandable in terms of a two-state model. In the remainder of the paper, we concentrate on designing effective Hamiltonians which have physical solutions identical to those of the Schrödinger equation, but which have no unphysical states of lower energy than the physical ground state. We find that we must incorporate ideas from the Hirschfelder-Silbey perturbation theory, as modified by Polymeropoulos and Adams, to arrive finally at an effective Hamiltonian which promises to have the desired properties, namely, that all unphysical states be higher in energy than the physical bound states, that the first and higher order corrections to the energy vanish in the limitR = ∞. that the leading terms of the asymptotic 1/R expansion of the energy be given correctly in second order, and that the overlap between the zeroth order wave function and the corresponding eigenfunction of the effective Hamiltonian be close to one.