A tandem Jackson network with feedback to the first node

Abstract

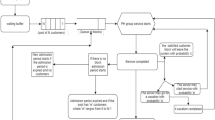
AnN-node tandem queueing network with Bernoulli feedback to the end of the queue of thefirst node is considered. We first revisit the single-nodeM/G/1 queue with Bernoulli feedback, and derive a formula forEL(n), the expected queue length seen by a customer at his nth feedback. We show that, asn becomes large,EL(n) tends to ρ/(l ρ), ρ being the effective traffic intensity. We then treat the entire queueing network and calculate the mean value ofS, the total sojourn time of a customer in theN-node system. Based on these results we study the problem ofoptimally ordering the nodes so as to minimize ES. We show that this is a special case of a general sequencing problem and derive sufficient conditions for an optimal ordering. A few extensions of the serial queueing model are also analyzed. We conclude with an appendix in which we derive an explicit formula for the correlation coefficient between the number of customers seen by an arbitrary arrival to anM/G/1 queue, and the number of customers he leaves behind him upon departure. For theM/M/1 queue this coefficient simply equals the traffic intensity ρ.