Thermal stresses and the shattering of solid particles in a shock layer

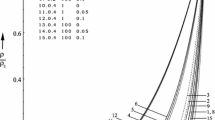
Abstract

The motion of blunt bodies through two-phase media at high supersonic velocities is accompanied by strong heating of particles when they enter the shock layer. Because the ratio of the heating time of nonmetallic particles to the time of their thermal relaxation with the gas exceeds unity, large temperature gradients are developed in the particles, which are stressed and deformed and under the influence of the force and inertial loads they can then shatter, which significantly changes their force and thermal effect on the supersonic body. A special case of this problem — the shattering of ice particles in a shock layer under the influence of pressure forces — was investigated in [1]. In the present paper, the results of numerical calculations and known analytic solutions are used in the development of an approximate method for estimating the stresses that arise in spherical particles. Simple criteria are established for determining when the tensile stresses in the particles reach critical values above which the particles may shatter. As an example, the distribution of the temperature and stresses in silicon dioxide particles is considered.