Abstract
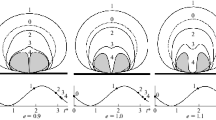
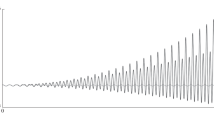
The evolution of the radius of a spherical cavitation bubble in an incompressible non-Newtonian liquid under the action of an external acoustic field is investigated. Non-Newtonian liquids having relaxation properties and also pseudoplastic and dilatant liquids with powerlaw equation of state are studied. The equations for the oscillation of the gas bubble are derived, the stability of its radial oscillation and its spherical form are investigated, and formulas are given for the characteristic frequency of oscillations of the cavitation hollow in a relaxing liquid. The equations are integrated numerically. It is shown that in a relaxing non-Newtonian liquid the viscosity may lead to the instability of the radial oscillations and the spherical form of the bubble. The results obtained here are compared with the behavior of a gas bubble in a Newtonian liquid.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
Rayleigh, “On pressure developed in a liquid during the collapse of a spherical cavity,” Phil. Mag., Ser. 6,34, No. 200 (1917).
B. E. Nolting and E. A. Neppiras, “Cavitation produced by ultrasonics,” Proc. Roy. Soc.,63B, 674 (1950).
H. G. Flynn, Physics of Acoustic Cavitation in Liquids. Physical Acoustics [Russian translation], Mir, Moscow (1967).
A. D. Pernik, Problems of Cavitation [in Russian], Sudostroenie, Leningrad (1966).
Physics and Technology of Intense Ultrasound. Intense Ultrasonic Fields [in Russian], Nauka, Moscow (1968).
M. S. Plesset, “On the stability of fluid flows with spherical symmetry,” J. Appl. Phys.,25, No. 1, 96 (1954).
M. S. Plesset and T. P. Mitchell, “On the stability of spherical shape of vapor cavity in a liquid,” Quart. Appl. Math.,13, No. 4 (1956).
Antony Eller and H. G. Flynn, “Generation of subharmonics of order one-half by bubbles in sound field,” J. Acoust. Soc. Am.,46, No. 3, Pt. 2, 722 (1969).
M. Reiner, Lectures on Theoretical Rheology, 3rd ed., North-Holland (1960).
Rheology. Theory and Application [Russian translation], IL, Moscow (1962).
V. A. Pavlovskii, “Problem of theoretical description of weak aqueous solutions of polymer,” Dokl. AN SSSR,200, No. 4, 809 (1971).
G. Houghton, “Theory of bubble pulsation and cavitation,” J. Acoust. Soc. Am.,35, No. 9, 1387 (1963).
V. G. Gasenko, V. E. Kolesnikov, and V. V. Sobolev, “Investigation of stability of spherical cavity in acoustic field,” Prikl. Mekhan. Tekh. i Fiz., No. 6 (1973).
A. V. Metzner, Non-Newtonian technology: fluid mechanics, mixing, and heat transfer, in: Advances in Chemical Engineering, Vol. 1, New York (1956).
Author information
Authors and Affiliations
Additional information
Translated from Izvestiya Akademii Nauk SSSR, Mekhanika Zhidkosti i Gaza, No. 2, pp. 129–135, March–April 1974.
The authors are thankful to I. R. Shreiber for assistance in the work.
Rights and permissions
About this article
Cite this article
Gasenko, V.G., Sobolev, V.V. Oscillations of a gas bubble in a non-Newtonian liquid under the action of an acoustic field. Fluid Dyn 9, 270–274 (1974). https://doi.org/10.1007/BF01092661
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01092661