Skip to main content
SpringerLink
Log in

Use of direct variational methods to optimize axisymmetric Laval nozzles in the case of equilibrium and nonequilibrium two-phase flows

  • Published:
Fluid Dynamics Aims and scope Submit manuscript

Abstract

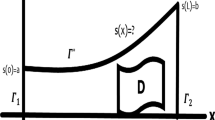
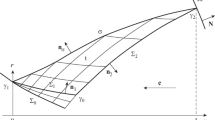
In the construction of the optimal profile of a Laval nozzle when there are subsonic regions in the flow, the use of effective methods such as the general method of Lagrangian multipliers [1] becomes very difficult. In the present paper, direct variational methods are therefore used. For nozzles, these methods were used for the first time to profile the supersonic parts of nozzles in the case of nonequilibrium two-phase flows by Dritov and Tishin [2]. For equilibrium flows, they have been used to optimize supersonic nozzles [3, 4] and in the construction of a profile of the subsonic part of a nozzle ensuring parallel sonic flow in the minimal section of the nozzle [3].

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature cited

  1. A. N. Kraiko, Variational Problems of Gas Dynamics [in Russian], Nauka, Moscow (1979), p. 447.

    Google Scholar 

  2. G. V. Dritov and A. P. Tishin, “Profiling of nozzles using gases with condensate particles,” Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza, No. 1, 170 (1971).

    Google Scholar 

  3. V. G. Butov, I. M. Vasenin, and A. I. Shelukha, “Use of methods of nonlinear programming to solve variational problems of gas dynamics,” Prikl. Mat. Mekh.,41, 59 (1977).

    Google Scholar 

  4. J. G. Allman and J. D. Heffman, “Design of maximum thrust nozzle contours by direct optimization methods,” AIAA Paper, No. 1048, 7 (1978).

    Google Scholar 

  5. G. V. R. Rao, “Approximation of optimum thrust nozzle contour,” ARS J.,30, 561 (1960).

    Google Scholar 

  6. D. A. Mel'nikov, U. G. Pirumov, and A. A. Sergienko, “Nozzles of jet engines,” in: Aerodynamics and Gas Dynamics [in Russian], Nauka, Moscow (1976), p. 57.

    Google Scholar 

  7. V. E. Alemasov, A. F. Dregalin, A. P. Tishin, and V. A. Khudyakov, Thermodynamic and Thermophysical Properties of Combustion Products, Vol. 1 [in Russian], Moscow (1971), p. 266.

    Google Scholar 

  8. A. A. Glazunov and A. D. Rychkov, “Investigation of nonequilibrium two-phase flows in axisymmetric Laval nozzles,” Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza, No. 6, 86 (1977).

    Google Scholar 

  9. R. K. Tagirov, “Theoretical investigation of the flow of an ideal gas in contracting nozzles,” Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza, No. 2, 198 (1978).

    Google Scholar 

  10. A. N. Kraiko and V. E. Sokolov, “On t specific impulse of the flow at the minimal section of a Laval nozzle and at the exit section of a contracting nozzle,” Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza, No. 1, 186 (1976).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Novosibirsk

    A. D. Rychkov

Authors
  1. A. D. Rychkov
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Izvestiya Akademii Nauk SSSR, Mekhanika Zhidkosti i Gaza, No. 1, pp. 181–183, January–February, 1982.

I thank A. N. Kraiko for a number of helpful comments in a discussion of the formulation of the problem.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rychkov, A.D. Use of direct variational methods to optimize axisymmetric Laval nozzles in the case of equilibrium and nonequilibrium two-phase flows. Fluid Dyn 17, 153–156 (1982). https://doi.org/10.1007/BF01090715

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01090715

Keywords

Search

Navigation