Abstract
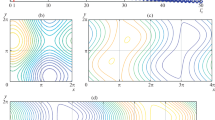
A new approach to the investigation of the nonlinear development of disturbances, based on the theory of invariant manifolds, is outlined. A method of obtaining projections of the Navier-Stokes equations on finite-dimensional invariant manifolds is proposed. The behavior of the disturbances is finally described by a system of ordinary differential equations with right sides in the form of power series in the amplitudes. It is an important property of the method that these series are convergent. A two-dimensional invariant projection is calculated numerically for plane Poiseuille flow. As a result, it is possible to clarify the nature of the change from subcritical to supercritical bifurcation and investigate new bifurcations of periodic flow regimes.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
A. Davey, “On Iton's finite amplitude stability theory for pipe flow,” J. Fluid Mech.,86, 695 (1978).
K. Stewartson and J. T. Stuart, “A non-linear instability theory for a wave system in plane Poiseuille flow,” J. Fluid Mech.,8, 529 (1971).
A. D. D. Craik, “Non-linear resonant instability in boundary layers,” J. Fluid Mech.,50, 393 (1971).
V. V. Struminskii, “Nonlinear theory of the development of aerodynamic disturbances,” Dokl. Akad. Nauk SSSR,153, 547 (1963).
V. V. Struminskii and B. Yu. Skobelev, “Nonlinear neutral curve for Poiseuille flow,” Dokl. Akad. Nauk SSSR,252, 566 (1980).
J. T. Stuart, “On the non-linear mechanics of wave disturbances in stable and unstable Parallel flows. Pt. 1,” J. Fluid Mech.,9, 353 (1960).
J. Watson, “On the non-linear mechanics of wave disturbances in stable and unstable parallel flows. Pt. 2,” J. Fluid Mech.,9, 371 (1960).
G. Iooss, “Théorie non linéaire de la stabilité des écoulements visqueux incompressibles,” Rech. Aerosp., No. 234, 7 (1970).
B. Yu. Skobelev and V. V. Struminskii, “Nonlinear development of disturbances in twodimensional laminar flows,” Prikl. Mat. Mekh.,41, 802 (1977).
V. I. Yudovich, “Onset of self-oscillation in fluids,” Prikl. Mat. Mekh.,35, 638 (1971).
B. Yu. Skobelev, “Analytic projection of nonlinear evolution equations on finite-dimensional invariant manifolds,” Preprint No. 22–86 [in Russian], Institute of Theoretical and Applied Mechanics, Siberian Branch of the USSR Academy of Sciences, Novosibirsk (1986).
J. Marsden and M. McCracken, The Hopf Bifurcation and its Application, Springer, New York (1976).
W. C. Reynolds and M. C. Potter, “Finite-amplitude instability of parallel shear flows,” J. Fluid Mech.,27, 465 (1967).
I. P. Andreichikov and V. I. Yudovich, “Self-oscillatory regimes branching from Poiseuille flow in a plane channel,” Dokl. Akad. Nauk SSSR,202, 791 (1972).
B. Yu. Scobelev and Yu. I. Molorodov, “Subcritical autooscillations and nonlinear neutral curve for Poiseuille flow,” Comput. Math. Appl.,6, 123 (1980).
T. Poston and I. Stewart, Catastrophe Theory and its Application, London (1978).
Author information
Authors and Affiliations
Additional information
Translated from Izvestiya Akademii Nauk SSSR, Mekhanika Zhidkosti i Gaza, No. 1, pp. 9–15, January–February, 1990.
The author is grateful to A. Zharilkasinov for carrying out the numerical calculations.
Rights and permissions
About this article
Cite this article
Skobelev, B.Y. Nonlinear theory of hydrodynamic stability and bifurcations of solutions of the Navier-Stokes equations. Fluid Dyn 25, 6–11 (1990). https://doi.org/10.1007/BF01051290
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01051290