The problem of supersonic flow over the lower surface of a triangular wing

Abstract

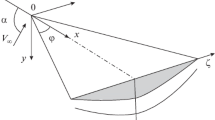
In formulating the problem we make no assumption of smallness of the angle of attack; the attached three-dimensional compression shock which arises under the lower surface of the wing may be of arbitrary intensity, and in form is assumed to differ little from a plane shock; a finite yaw angle is allowed. We consider linear supersonic conical flow which is realized, with the exception of a characteristic linear dimension, in the portion of space bounded by the shock, the plane of the wing, and the surface of a disturbance cone with vertex at the discontinuity of the supersonic leading edge and which is a disturbance of the uniform flow behind the plane shock wave.

The problem studied reduces to the homogeneous Hilbert boundary-value problem for an analytic function of a complex variable, whose real and imaginary parts are the partial derivatives of the unknown pressure disturbance with respect to the similarity coordinates.

In the solution of the boundary-value problem, the effective method of Lighthill, developed with application to diffraction problems [1, 2], is generalized to the problem of an asymmetric region.

The particular case of hypersonic flow about an unyawed triangular wing has been studied by Malmuth [3]; the author obtains the problem considered by Lighthill in [2] and writes out the solution contained in that work.