Abstract
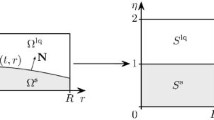
We consider two different time discretization algorithms for a nonlinear parabolic PDE arising in heat conduction phenomena with phase changes in two adjoining bodies Ω and Γ, where Γ can be considered as the boundary of Ω. Stability, convergence and error estimate results are given for both algorithms.
Sommario
Si studiano due algoritmi di discretizzazione nel tempo di un sistema di equazioni a derivate parziali non lineari paraboliche che governa la conduzione del calore, in presenza di cambiamento di fase, in due corpi congiunti Ω e Γ, di cui Γ possa essere considerato come la frontiera di Ω, Vengono dati risultati di stabilità, convergenza e maggiorazione dell'errore per entrambi gli algoritmi.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Amiez, G. and Grémaud, P. A., ‘On a numerical approach of Stefanlike problems’,Numer. Math.,59 (1991) 71–89.
Andreucci, D., ‘Existence and uniqueness of solution to a concentrated capacity problem with change of phase’,European J. Appl. Math.,1, (1990) 339–351.
Berger, A. E., Brézis, H. and Rogers, J. C. W., ‘A numerical method for solving the problemu t - Δf(u) 0’RAIRO Modél. Math. Anal. Numér.,13 (1979) 297–312.
De Rham, G.,Variétés Differentiables, Hermann, Paris, 1955.
Fasano, A., Primicerio, M. and Rubinstein, L., ‘A model problem for heat conduction with a free boundary in a concentrated capacity’,J. Inst. Maths. Appl.,26 (1980) 327–347.
Jäger, W. and Kačur, J., ‘Solution of porous medium type systems by linear approximation schemes’,Numer. Math.,60 (1991) 407–427.
Lions, J. L. and Magenes, E.,Non-Homogeneous Boundary Value Problems and Applications, Vols 1 and 2, Springer-Verlag, Berlin, 1972.
Magenes, E., ‘Remarques sur l'approximation des problèmes non linéaires paraboliques’, inAnalyse Mathématique et Applications, Gauthier-Villars, Paris, 1988, pp. 298–318.
Magenes, E., ‘Numerical approximation of nonlinear evolution problems’, inFrontiers in Pure and Applied Mathematics (ed. R. Dautray), North-Holland, Amsterdam, 1991, pp. 193–207.
Magenes, E., ‘Some new results on a Stefan problem in a concentrated capacity’,Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. (9,3 (1992) 23–34.
Magenes, E., ‘The Stefan problem in a concentrated capacity’, inProc. Internat. Symp. on Problemi attuali dell'Analisi e della Fisica Matematica dedicated to G. Fichera, Taormina, 1992 (to appear).
Magenes, E., Nochetto, R.H. and Verdi, C., ‘Energy error estimates for a linear scheme to approximate nonlinear parabolic equations’,RAIRO Modél. Math. Anal. Numér.,21 (1987) 655–678.
Nochetto, R. H., ‘A stable extrapolation method for multidimensional degenerate problems’,Math. Comput.,53 (1989) 455–470.
Nochetto, R. H. and Verdi, C., ‘An efficient linear scheme to approximate parabolic free boundary problems: error estimates and implementation’,Math. Comput.,51 (1988) 27–53.
Shillor, M., ‘Existence and continuity of a weak solution to the problem of a free boundary in a concentrated capacity’,Proc. Roy. Soc. Edinburgh Sect. A,100 (1985) 271–280.
Slodička, M., ‘Solution of nonlinear parabolic problems by linearization’, Preprint n. M3-92Comenius Univ. Fuc. Math. Phys. (1992) 1–9.
Verdi, C. and Visintin, A., ‘Error estimates for a semi-explicit numerical scheme for Stefan-type problems’,Numer. Math.,52 (1988) 165–185.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Magenes, E., Verdi, C. Time discretization schemes for the Stefan problem in a concentrated capacity. Meccanica 28, 121–128 (1993). https://doi.org/10.1007/BF01020324
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01020324