Skip to main content
SpringerLink
Log in

Rheological behaviour of fresh cement paste as measured by squeeze flow

  • Papers
  • Published:
Journal of Materials Science Aims and scope Submit manuscript

Abstract

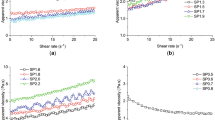
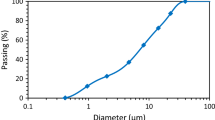
A method is proposed for measuring the rheology of cement paste under conditions that suppress shear flow, i.e. squeezing. This method is based on squeezing samples in a servohydraulic compression-tension testing machine, and is different from the commonly used shear flow experiments. Possible artefacts such as the buoyancy of the piston that penetrates the paste, sedimentation of cement paste, geometry of the container, and friction at the interface between the top plate (or piston) and sample are investigated. Plots of stress versus apparent strain were obtained and compared with results from standard shear flow experiments. Because cement paste has both viscoelastic and viscoplastic characteristics, results are analysed in terms of both solid-like deformation and liquid-like flow behaviour. A first-approximation theoretical analysis is developed, based on the assumption that cement paste behaves as a non-Newtonian liquid, and results are compared with the experimental results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

\(\dot \gamma\) :

Shear strain rate in power law fluid model

γ zr :

Shear strain converted from ε zr

\(\dot \gamma _{zr}\) :

Shear strain rate

έ:

Normal strain rate

ε zr :

Component of shear strain

έ zr :

Component of shear strain rate

ε zz :

Component of normal strain

η:

Viscosity

ϱ:

Density of cement paste (3.2 g cm−3)

σCav :

Calculated average normal stress of cement paste

σNav :

Calculated average normal stress of power law fluid

σm :

Measured normal stress of cement paste

σ zz :

Normal stress in z direction

Τeq :

Equivalent shear stress converted from normal stress

Τ rz :

Shear stress in momentum equation

a i :

Coefficients in polynomial function of geometric factor for cement paste

B :

Buoyancy force

CGF :

Geometric factor for cement paste

d o :

Amplitude of squeeze motion

F N :

Load in normal direction

g :

Gravitational constant

h :

Sample height

h o :

Initial sample height

\(\dot h\) :

Velocity of platen

k :

Order of polynomial function of geometric factor for cement paste

m :

Consistency in power-law fluid model

n :

Power index in power-law fluid model

P :

Pressure

P a :

Atmospheric pressure

PGF :

Geometric factor for power-law fluid model

r :

Radial direction in cylindrical coordinates

R :

Radius of sample

s :

1/n

V :

Volume of the top platen submerged into cement paste

v r :

Velocity inr direction

v z :

Velocity in z direction

z :

Vertical direction in cylindrical coordinates

References

  1. B. H. Min, L. Erwin, andH. M. Jennings,Ceram. Trans. 16 (1990) 337.

    Google Scholar 

  2. Idem,Korean J. of Rheol., in press.

  3. G. H. Tattersall,Nature 175 (1955) 166.

    Google Scholar 

  4. R. Lapsin,Cemento 4 (1982) 243.

    Google Scholar 

  5. W. Vom Berg, in Proceedings of 8th Internationl Congress on Rheology, Vol. 3 (Plenum, New York, 1980) p. 665.

    Google Scholar 

  6. I. Odler, T. Becker andB. Weiss,Cemento (1978) 303.

  7. P. F. G. Banfill,Mag. Concr. Res. 33 (1981) 37.

    Google Scholar 

  8. T. E. R. Jones, G. Brindly andB. C. Patel, in “Hydraulic Cement Pastes: Their Structure and Properties”, Proceedings of Conference, University of Sheffield, 1976, p. 135.

  9. A. R. Cusen andJ. Harris, in Proceedings of RILEM, on “Fresh concrete; important properties and their measurements, Sem”. Leeds, England, 1973. Vol. 1 (Dept. of Civil Engng. University of Leeds, Leeds, England, 1973) p. 2.8.1.

    Google Scholar 

  10. T. M. Chow, L. V. McIntire, K. R. Kunze andC. E. Cooke,SPE Prodn Engng 3(4) (1988) 543.

    Google Scholar 

  11. P. F. G. Banfill andD. R. Kitching, in Proceedings of International Congress on Rheology of Fresh Cement and Concrete, edited by P. F. G. Banfill (University Press, Cambridge, 1991) p. 125.

    Google Scholar 

  12. G. J. Dienes andH. F. Klemm,J. Appl. Phys. 17 (1946) 458.

    Google Scholar 

  13. G. J. Dienes,J. Coll. Sci. 2 (1947) 131.

    Google Scholar 

  14. R. J. Grimm,AIChE J. 24 (1978) 427.

    Google Scholar 

  15. K. S. Gandhi andR. Burns,Trans. Soc. Rheol. 20 (1976) 489.

    Google Scholar 

  16. R. J. Silva-Nietto, B. C. Fisher andA. W. Birly,Polym. Engng Sci. 21 (1981) 499.

    Google Scholar 

  17. E. J. Dickenson andH. P. Witt,Trans. Soc. Rheol. 13 (1969) 485.

    Google Scholar 

  18. A. N. Gent,Br. J. Appl. Phys. 11 (1960) 85.

    Google Scholar 

  19. M. J. Foster,J. Appl. Phys. 26 (1955) 1104.

    Google Scholar 

  20. S. H. Chatraei, C. W. Macosko andH. H. Winter,J. Rheol. 25 (1981) 433.

    Google Scholar 

  21. A. Terentyev andG. Kunnos, in Proceedings of International Congress on Rheology of Fresh Cement and Concrete, edited by P.F.G. Banfill (Cambridge University Press, Cambridge, 1990) p. 93.

    Google Scholar 

  22. M. Reiner, in “Rheology”, Vol. 3, edited by F. R. Eirich (Academic, New York, 1960) p. 351.

    Google Scholar 

  23. R. B. Bird, R. C. Armstrong andO. Hassager, “Dynamics of Polymeric Liquids”, Vol. 1, (Wiley, New York 1977) p. 429.

    Google Scholar 

  24. W. Ostwald, V. Kolloid-Z. 36 (1925) 99.

  25. A. De Waele,Oil & Color Chem. Assoc. J. 6 (1923) 23.

    Google Scholar 

  26. P. J. Leider andR. B. Bird, in “Industrial Engineering Chemical Fundamentals”, Vol. 13 (American Chemical Society, Washington, 1974) p. 336.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departments of Mechanical Engineering, Robert R. McCormick School of Engineering and Applied Science, Northwestern University, 60208, Evanston, Illinois, USA

    B. H. Min

  2. Departments of Material Science and Engineering, Robert R. McCormick School of Engineering and Applied Science, Northwestern University, 60208, Evanston, Illinois, USA

    L. Erwin

  3. Civil Engineering, Robert R. McCormick School of Engineering and Applied Science, Northwestern University, 60208, Evanston, Illinois, USA

    H. M. Jennings

Authors
  1. B. H. Min
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. Erwin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H. M. Jennings
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Min, B.H., Erwin, L. & Jennings, H.M. Rheological behaviour of fresh cement paste as measured by squeeze flow. J Mater Sci 29, 1374–1381 (1994). https://doi.org/10.1007/BF00975091

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00975091

Keywords

Search

Navigation