Skip to main content
SpringerLink
Log in

Transient behaviors of natural convective heat transfer through a vertical porous layer

  • Published:
Applied Scientific Research Aims and scope Submit manuscript

Abstract

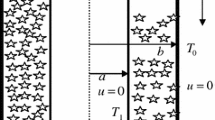
The present investigation is devoted to study numerically and experimentally on the transient behaviors of natural convective heat transfer in a rectangular cavity (whose two opposing vertical walls are kept at uniform (but different) temperatures, while the other walls are thermally insulated) packed with a fluid and spherical solid particles. The natural convection occurred in dependence on the dimensions of the cavity, the diameter of the solid particle and the thermal physical properties of the porous media plays an important role in an evaluation of the transient behaviors of the heat transfer in the porous layer. It can be clarified that the natural convection occurring in the porous layer has the effects of homogenizing thermally the porous layer and shortening the time period to reach a thermally steady state after starting the heating to porous layer. Consequently it might be possible to control the transient time period and the amount of heat stored into the porous layer by managing the intensity of natural convection with proper combinations of fluid and solid particles and dimensions of the cavity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A, B, C :

arbitrary constants in equation (7)

a :

thermal diffusivity

a*:

modified thermal diffusivity, λ*/(ρc ρ ) f

c p :

specific heat at constant pressure

D :

non-dimensional heat transfer coefficient in (6)

d :

mean diameter of spherical solid particle

E :

volumetric ratio of solid phase to fluid phase in (6)

G :

constant, (1.75dρ f )/[150k(1−ε)]

g :

gravitational acceleration

H :

height of rectangular cavity

H/W :

aspect-ratio

h :

heat transfer coefficient per unit volume between fluid and solid phases

k :

permeability

L :

heat capacity ratio of solid phase to fluid phase in (6)

Nu * h , Nu * c :

modified Nusselt number at hot and cold walls in (12) and (13), respectively

Nu*:

modified Nusselt number at steady state

n :

number of iteration computation

Pr*:

modified Prandtl number

p :

pressure

Ra*:

modified Rayleigh number

T :

temperature

ΔT :

temperature difference between hot and cold walls, (T h −T c )

t :

time

U, V :

velocity in theX andY directions, respectively

W :

width of rectangular cavity

X, Y :

co-ordinates

β :

cubical thermal expansion coefficient

ψ :

stream function

Ψ:

non-dimensional stream function

ε :

porosity

λ:

thermal conductivity

λ*:

effective thermal conductivity of porous medium (without convection)

λ * f :

effective thermal conductivity resulted from the contribution of fluid phase to λ*

λ * s :

effective thermal conductivity resulted from the contribution of solid phase to λ*

Λ:

non-dimensional thermal conductivity in (6)

ν :

kinematic viscosity

ρ :

density

τ :

non-dimensional time in (6)

δ :

relaxation factor

c, h :

cold and hot walls, respectively

f, s :

fluid and solid phases, respectively

i, j :

grid points of computative mesh in theX* andY* directions, respectively

*:

non-dimensional value excepta, λ, λ f and λ s

References

  1. Combarnous MA and Bories SA (1975) Advances in Hydrosciences 10. Academic Press.

  2. Combarnous MA (1978) 6th International Heat Transfer Conference, Toronto p. 45.

  3. Simpkins PG and Blythe PA (1980) Int J Heat Mass Trans 23: 881.

    Google Scholar 

  4. Bories SA and Deltour A (1980) Int J Heat Mass Trans 23: 765.

    Google Scholar 

  5. Elder JW (1967) J Fluid Mech 27: 609.

    Google Scholar 

  6. Holst PH and Aziz K (1972) The Canadian J of Chemical Engng 50: 232.

    Google Scholar 

  7. Holst PH and Aziz K (1972) Int J Heat Mass Trans 15: 73.

    Google Scholar 

  8. Schneider KJ (1963) 11th International Congress on Refrigeration, Paper No 11-4, Munich.

  9. Seki N, Fukusako S and Ariake Y (1979) Trans Japan Soc Mech Eng 45: 705.

    Google Scholar 

  10. Brinkman HC (1947) Appl Sci Res A1: 27

    Google Scholar 

  11. Rudraiah N, Veerappa B and Balachandra Rao A (1980) J of Heat Transfer, ASME 102: 254.

    Google Scholar 

  12. Vafai K and Tien CL (1981) Int Heat Mass Trans 24: 195.

    Google Scholar 

  13. Ergun S (1952) Chemical Engineering Progress 48 (2): 89.

    Google Scholar 

  14. Combarnous MA and Bories SA (1974) Int J Heat Mass Trans 17: 505.

    Google Scholar 

  15. Kunii D and Smith JM (1960) A I Ch E Journal 6: 71.

    Google Scholar 

  16. Schlichting H (1968) Boundary-Layer Theory. McGraw-Hill

  17. Hennecke DK, Sparrow EM and Eckert ERG (1971) Wärme-und Stöffubertragung 4: 222.

    Google Scholar 

  18. Silveston PL (1958) Forch Geb Ing Wes 24: 26.

    Google Scholar 

  19. Seki N, Fukusako S and Inaba H (1978) Int J Heat Mass Trans 21: 985.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Kitami Institute of Technology, Kitami, 090, Hokkaido, Japan

    Hideo Inaba

  2. Department of Mechanical Engineering, Faculty of Engineering, Hokkaido University, 060, Sapporo, Japan

    Nobuhiro Seki

Authors
  1. Hideo Inaba
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nobuhiro Seki
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Inaba, H., Seki, N. Transient behaviors of natural convective heat transfer through a vertical porous layer. Appl. Sci. Res. 37, 257–273 (1981). https://doi.org/10.1007/BF00951251

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00951251

Keywords

Search

Navigation