Abstract
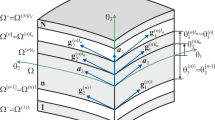
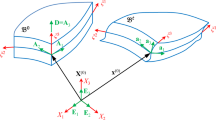
A new approach for three-dimensional stress analyses in composite cylindrical shells is presented. The method of composite expansions along with Hellinger-Reissner variational formulation is employed to derive the interior and edge layer problems for high order approximations. Classical assumptions have been justified and new approximations have been established. These formulations are directed especially towards, new high integrity mixed-hybrid finite element schemes. The expository examples chosen are of cross-ply and angle-ply laminated shells. The circumferential location of the delamination failure initiation, for angle-ply laminates containing a circular hole, is within a sector located symmetrically around the perpendicular direction to the applied load.
Similar content being viewed by others
References
H. V. Lakshminarayana and S. Viswanath,A high precision triangular laminated anisotropic cylindrical shells finite element. Computers & Struc.8, 633–640 (1978).
P. Van-Dyke,Stresses about a circular hole in a cylindrical shell. AIAA J.3, No. 9, 1733–1742 (1965).
M. V. V. Murthy,Stresses around an elliptic hole in a cylindrical shell. J. Appl. Mech., ASME36, 39–46 (1969).
G. N. Savin.Concentration of stresses around curvilinear holes in plates and shells. Proc. of the 11th Int. Conference of Appl. Mech. 269–296 (1964).
M. Sayir and C. Mitropoulos,On elementary theories of linear elastic beams, plates, and shells (Review paper). J. Appl. Math. Phys. (ZAMP)31, 1–55 (1980).
M. W. Johnson and E. Reissner,On the foundations of the theory of thin elastic shells. J. Math. and Phys.37, 374–392 (1956).
E. L. Reiss,A theory for the small rotationally symmetric deformations of cylindrical shells. Comm. on Pure and Appl. Math. XIII, 531–550 (1960).
A. E. Green,Boundary layer equations in the linear theory of thin elastic shell. Proc. of the Royal Soc. London,A269, 481–491 (1962).
A. L. Gol'denveizer,Boundary layer and its interaction with the interior state of stress of an elastic thin shell. PMM33, No. 6 996–1028 (1969).
M. Sayir,Edge effects in rotationally symmetric composite shells. “Local Effects in the Analysis of Structures” (ed. P. Ladevèze). Elsevier Publ., Essex (1985).
P. Bar-Yoseph and J. Avrashi,Interlaminar stress analysis for laminated plates containing a curvilinear hole. Computers & Struc.21, 917–932 (1985).
P. Bar-Yoseph and G. Siton,The effect of material non-linearity on the interlaminar stress field in composite laminates. Computers & Struc.21, 1105–1118 (1985).
E. Reissner,On a variational theorem in elasticity. J. Math. Phys.29, 90–95 (1950).
G. E. Widera and D. L. Logan,Refined theories for nonhomogeneous anisotropic cylindrical shells: I. Derivation II. Application. Engng. Mech. Div., ASCE106, EM6, 1053–1090 (1980).
P. Bar-Yoseph and J. Avrashi,New variational-asymptotic formulation for interlaminar stress analysis in laminated plates. J. Appl. Math. Phys. (ZAMP)37, 305–321 (1986).
P. Bar-Yoseph and J. Avrashi,On the nature of the free edge stress singularity in composite laminated plates. Int. J. Numer. Meth. Eng. (in press).
I. Babuska,Error bounds for finite element method. Numer. Math.16, 322–333 (1971).
F. Brezzi,On the existence, uniqueness and approximation of saddle point problems arising from Lagrangian multipliers. R.A.I.R.O., Anal. Numer.8-R2, 129–151 (1974).
K. Washizu,Variational methods in elasticity and plasticity. Pergamon Press, New York 1982.
T. H. H. Pian, D. P. Chen and D. Kang,A new formulation of hybrid/mixed finite element. Computers & Struct.16, 81–87 (1983).
E. F. Punch and S. N. Atluri,Applications of isoparametric three-dimensional hybrid-stress finite elements with least-order stress fields. Computers and Struc.19, 409–430 (1984).
T. H. H. Pian and D. P. Chen,On the suppression of zero energy deformation modes. Int. J. Numer. Meth. Engng.19, 1741–1752 (1983).
P. Bar-Yoseph,On the accuracy of interlaminar stress calculation in laminated plates. Comput. Meth. Appl. Mech. Engng.36, 309–329 (1983).
P. Bar-Yoseph and J. Avrashi,Variational-asymptotic formulation for 3-D stress analysis of free edge problems in laminated composites. Proc. Int. Conf. on Computational Eng. Sci. (ICES '88) (S. N. Atluri and G. Yagawa eds.), to be held at Atlanta, Georgia, 10–14 April 1988.
I. S. Raju and J. H. Crews,Three-Dimensional Analysis of [0/90] s and [90/0] s Laminates with a Central Circular Hole”, Compos. Technol. Rev.4, 116–124 (1981).
F. Lene,Damage constitutive relations for composite materials. Eng. Frac. Mech.25, 713–728 (1986).
P. Bar-Yoseph, G. Yaniv and O. Ishai,The interdependence of hygrothermal processes and elasto-viscoplastic behaviour in polymer-dominated multi-material systems. Computers & Struc.25, 11–27 (1987).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Bar-Yoseph, P., Avrashi, J. New variational-asymptotic formulations for 3-D stress analyses of laminated composite shells with a circular hole. Z. angew. Math. Phys. 39, 682–698 (1988). https://doi.org/10.1007/BF00948730
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00948730