General Weissenberg effect in free surface rheometry part I: analytical considerations

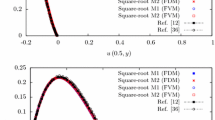
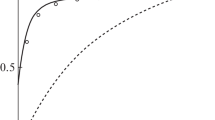
Summary

The steady free surface motion of a layered medium of viscoelastic fluids driven by a vertical rotating rod and the free surface motion of a viscoelastic fluid between vertical, eccentric, rotating cylinders is solved by means of domain perturbations. The flow field, the shape of the free surfaces and the interface and the climb at the rod are determined by expanding the stress in a series of Rivlin-Ericksen tensors and developing the theory as a perturbation of the rest state in powers of the angular frequencyΩ of the rod or of the cylinders. It is shown that rheometrical measurements in the rotating rod geometry are reliably reproducible whilst concentric cylinder geometry presents important practical problems in measuring rheological constants.

Résumé

Les problèmes des écoulements stationnaires à surface libre de plusieurs couches superposées de fluides viscoélastiques mis en mouvement par une barre verticale en révolution et d'un fluide viscoélastique entre des cylindres verticaux, excentriques et tournants sont résolus par le moyen des perturbations de domaine. Le champ des vitesses, les formes de la surface libre et de l'interface sont déterminées en développant la contrainte en une série de tenseurs Rivlin-Ericksen. La théorie est basée sur la perturbation de l'état statique et les variables sont exprimées en une série de puissances de la vitesse de rotation de la barre ou des cylindres. On a démontré que les mesurements rhéométriques dans la géométrie de barre tournante sont sûrement reproductibles tandis que l'utilisation de la géométrie de cylindres concentriques présente d'importants problèmes pratiques en mesurant les constantes rhéologiques.