Skip to main content
SpringerLink
Log in

A technique for time-dependent boundary value problems in the kinetic theory of gases part II. Application to sound propagation

  • Original Papers
  • Published:
Zeitschrift für angewandte Mathematik und Physik ZAMP Aims and scope Submit manuscript

Abstract

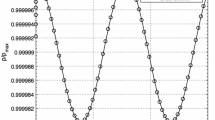
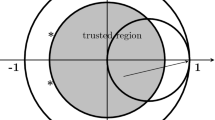
Following the procedure indicated in part I, a canonical solution of the matrix Riemann-Hilbert problem for sound propagation in a gas occupying a half space is presented. The closed form solution is computed numerically for three particular values of the sound frequency. The results compare favorably with a previously known numerical solution.

Sommario

Seguendo il procedimento indicate nella prima parte, si presenta una soluzione canonica del problema matriciale di Riemann-Hilbert per la propagazione del suono in un gas che occupa un semispazio. La soluzione viene poi calcolata numericamente per tre valori particolari della frequenza. I risultati sono in buon accordo con una precedente soluzione numerica.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. C. S. Wang Chang and G. E. Uhlenbeck, inStudies in statistical mechanics, Vol. V. North Holland, Amsterdam 1970.

    Google Scholar 

  2. C. L. Pekeris, Z. Alterman, L. Finkelstein, and K. Frankowski, Phys. Fluids5, 1608 (1962).

    Google Scholar 

  3. L. Sirovich and K. Thurber, J. Acoust. Soc. Am. 37, 329 (1965).

    Google Scholar 

  4. J. K. Buckner and J. H. Ferziger, Phys. Fluids9, 2315 (1966).

    Google Scholar 

  5. R. J. Mason, inRarefied gas dynamics, edited by J. H. de Leeuw. Academic Press, New York 1965, Vol. 1, p. 48.

    Google Scholar 

  6. S. K. Loyalka and T. C. Cheng, Phys. Fluids22, 830 (1979).

    Google Scholar 

  7. J. R. Thomas, Jr. and C. E. Siewert, Trans. Theory and Stat. Phys.8, 219 (1979).

    Google Scholar 

  8. C. Cercignani,Theory and application of the Boltzmann equation. Scottish Academic Press, Edinburgh and Elsevier, New York 1975, p. 334.

    Google Scholar 

  9. C. E. Siewert and E. E. Burniston, J. Math. Phys.18, 376 (1977).

    Google Scholar 

  10. C. E. Siewert and E. E. Burniston, Z. angew. Math. Phys.30, 1005 (1979).

    Google Scholar 

  11. C. Cercignani, Trans theory and stat. phys.6, 29 (1977).

    Google Scholar 

  12. C. E. Siewert and C. T. Kelley, Z. angew. Math. Phys.31, 334 (1980).

    Google Scholar 

  13. C. E. Siewert, C. T. Kelley, and R. D. M. Garcia, J. Math. Anal. Appl.84, 509 (1981).

    Google Scholar 

  14. C. E. Siewert and J. R. Thomas, Jr., Z. angew. Math. Phys.33, 473 (1982).

    Google Scholar 

  15. K. Aoki and C. Cercignani, Z. angew. Math. Phys.35, 127 (1984).

    Google Scholar 

  16. N. I. Muskhelishvili,Singular integral equations. Noordhoff, Groningen 1953.

    Google Scholar 

  17. R. J. Mason, Phys. Fluids13, 1467 (1970).

    Google Scholar 

  18. C. E. Siewert, E. E. Burniston, and J. R. Thomas, Jr., Phys. Fluids16, 1532 (1973).

    Google Scholar 

  19. C. Cercignani and C. E. Siewert, Z. angew. Math. Phys.33, 297 (1982).

    Google Scholar 

  20. J. R. Thomas, Jr. and C. E. Siewert, private communication.

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica, Politecnico di Milano, Milano, Italy

    K. Aoki & C. Cercignani

Authors
  1. K. Aoki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C. Cercignani
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

On leave from the Department of Aeronautical Engineering, Kyoto University, Kyoto 606, Japan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Aoki, K., Cercignani, C. A technique for time-dependent boundary value problems in the kinetic theory of gases part II. Application to sound propagation. Z. angew. Math. Phys. 35, 345–362 (1984). https://doi.org/10.1007/BF00944883

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00944883

Keywords

Search

Navigation