Abstract
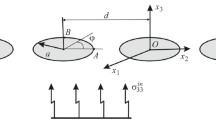
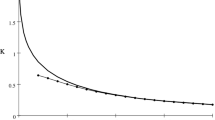
The axisymmetric interaction problem of an elastic spherical inclusion with a penny-shaped crack in an elastic space under torsion is considered. The superposition and reflection methods [3]-[4] are used to solve the mixed boundary value problem in question. With the help of the dual integral equations technique and appropriate re-expansion of the eigenfunction, the problem is reduced to an infinite system of linear algebraic equations of the second kind. The matrix elements of that system decrease exponentially along the rows and the columns. Its unique solution is proved to exist in a proper class of sequences and is shown to be represented by a convergent, in the vicinity of the origin, power series in a geometric parameter, equal to the ratio of the radius of the inclusion to its distance from the crack. This procedure provides an efficient formula for the stress intensity factor.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
C. Atkinson,The interaction between a crack and an inclusion, Int. J. Engng. Sci.,10, 127–136 (1972).
F. Erdogan, G. D. Gupta and M. Ratwani,Interaction between a circular inclusion and an arbitrary oriented crack, J. Appl. Mech.,41, 1007–1013 (1974).
Yu. A. Godin and A. S. Zil'bergleit,Axisymmetric electrostatic problem of a dielectric sphere near a conducting plane. Sov. Phys., Tech. Phys.,31 (6), 632–637 (1986).
Yu. A. Godin and A. S. Silbergleit,Axially symmetric contact torsion problem for elastic half-space with elastic spherical inclusion, Preprint # 1335, A. F. Ioffe Phys. Tech. Inst., Leningrad 1989 (in Russian).
V. S. Protsenko and A. I. Solov'yev,On some expansion formulae in the theory of harmonic junctions and its application to the solving of boundary value problems. Mathematical Methods of Analyzing of Dynamic Systems,8, Khar'kov, 50–77 (1984) (in Russian).
G. N. Watson,A Treatise on the Theory of Bessel Functions, 2nd ed., Cambridge University Press, London 1962.
A. T. Erofeenko,Addition Theorems, Nauka i Tekhnika, Minsk 1988 (in Russian).
Ya. S. Uflyand,Method of Dual Equations in Mathematical Physics Problems, Nauka, Leningrad 1977 (in Russian).
L. V. Kantorovich and V. I. Krylov,Approximate Methods of Higher Analysis, Noordhof, New York 1964.
I. N. Sneddon and M. Lowengrub,Crack Problem in the Classical Theory of Elasticity, John Wiley and Sons, Inc., New York 1969.
H. Bateman and A. Erdélyi,Higher Transcendental Functions. Vol. I, McGraw-Hill, New York 1955.
H. Bateman and A. Erdĺyi.Higher Transcendental Functions, Vol. II. McGraw-Hill, New York 1955.
A. Erdélyi et al.,Tables of Integral Transforms, Vol. I, McGraw-Hill, New York 1954.
A. Erdélyi et al.,Tables of Integral Transforms, Vol. II, McGraw-Hill, New York 1954.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Godin, Y.A. The interaction between a penny-shaped crack and a spherical inclusion under torsion. Z. angew. Math. Phys. 46, 932–945 (1995). https://doi.org/10.1007/BF00917878
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00917878