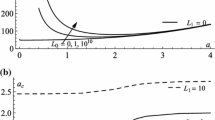
Abstract
Convective instability of equilibrium in a system of two horizontal layers of immiscible liquids, caused by the Rayleigh instability mechanism, has been studied within the framework of the linear theory in [1–5]. The present study will investigate the effect of a surface-active material (SAM), deposited on the boundary between the liquids, on the development of thermogravitation convection. Calculations were performed for two types of systems, which in the absence of a SAM show instability of a monotonic or an oscillatory character. A new type of oscillatory equilibrium instability was observed, produced by the effect of the SAM. In some region of parameter values the oscillatory instability may prove to be the more dangerous one. The action of the Marangoni effect on thermogravitation oscillations is considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
R. W. Zeren and W. C. Reynolds, “Thermal instabilities in two-fluid horizontal layers,” J. Fluid Mech.,53, No. 2 (1972).
E. I. Berezovskii, T. L. Perel'man, and E. A. Romashko, “Convective instability in a system of two inorganic horizontal layers of immiscible liquids,” Inzh. Fiz. Zh.,27, No. 6 (1974).
E. N. Ferm and D. J. Wollkind, “Onset of Rayleigh-Bernard-Marangoni instability: comparison between theory and experiment,” J. Non-Equilib. Thermodyn.,7, No. 3 (1982).
G. Z. Gershun and E. M. Zhukhovitskii, “Monotonic and oscillatory instability of a two-layer system of immiscible liquids heated from below,” Dokl. Akad. Nauk SSSR,265, No. 2 (1982).
G. Z. Gershun, E. M. Zhukhovitskii, and E. A. Pershina, “Development of convection in some two-layer systems,” in: Convective Flows [in Russian], Perm' (1983).
A. A. Nepomnyashchii, “Longwave convective instability in horizontal layers with a deformed boundary,” in: Convective Flows [in Russian], Perm' (1983).
V. G. Levich, Physicochemical Hydrodynamics [in Russian], Izd. Akad. Nauk SSSR, Moscow (1952).
J. C. Berg and A. Acrivos, “The effect of surface-active agents on convection cells induced by surface tension,” Chem. Eng. Sci.,20, 737 (1965).
M. Hennenberg, P. M. Bisch, et al., “Mass transfer. Marangoni effect and instability of interfacial longitudinal waves. I. Diffusional exchanges,” J. Colloid Interface Sci.,69, No. 1 (1979).
M. Hennenberg, P. M. Bisch, et al., “Mass transfer Marangoni effect and instbility of interfacial longitudinal waves. II. Diffusional exchanges and adsorption-desorption processes,” J. Colloid Interface Sci.,74, No. 2 (1980).
M. Hennenberg, A. Sanfeld, and P. M. Bisch, “Adsorption-desorption barrier, diffusional exchanges, and surface instabilities of longitudinal waves for aperiodic regimes,” AIChE J.,27, No. 6 (1981).
A. A. Nepomnyashchii and I. B. Simanovskii, “Development of convection in a two-layer system,” in: Hydrodynamic and Convective Instability of an Incompressible Liquid [in Russian], Sverdlovsk (1984).
Author information
Authors and Affiliations
Additional information
Translated from Zhurnal Prikladnoi Mekhaniki i Tekhnicheskoi Fiziki, No. 5, pp. 76–81, September–October, 1986.
In conclusion, the authors express their gratitude to E. M. Zhukhovitskii for his helpful evaluation.
Rights and permissions
About this article
Cite this article
Gilev, A.Y., Nepomnyashchii, A.A. & Simanovskii, I.B. Development of thermogravitation convection in a two-layer system in the presence of a surface-active material on the boundary. J Appl Mech Tech Phys 27, 698–702 (1986). https://doi.org/10.1007/BF00916141
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00916141