Abstract
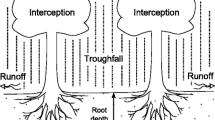
Of the recognized nonsteady-state factors that influence slope stability, probably most critical in many field situations is the character of precipitation and infiltration activity. A groundwater response model used in conjunction with precipitation records can provide a historical catalog of estimated maximum groundwater levels in a particular study area. An extreme-value statistical analysis of this catalog is linked with geotechnical slope stability analyses to provide a landslide hazard model for estimating the probability of slope failure within a given time. This modeling approach can provide meaningful input to risk assessments for landslide mitigation programs and to decision analyses and cost-benefit studies important for land-use planning and resource management.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Carr, J. R. and Bailey, R. E., 1986, An Indicator Kriging Model for Investigation of Seismic Hazard: Math. Geol., v. 18, p. 409–428.
Gumbel, E. J., 1958, Statistics of Extremes: Columbia University Press, New York, 375 p.
Kinnison, R. R., 1985, Applied Extreme Value Statistics: Battelle Press, New York, 149 p.
Kirsten, H. D. and Moss, A. S. E., 1985, Probability Applied to Slope Design—Case Histories,in C. H. Dowding (Ed.), Rock Masses—Modeling of Underground Openings/Probability of Slope Failure/Fracture of Intact Rock: ASCE, New York, p. 106–121.
Miller, S. M., 1984, Probabilistic Rock Slope Engineering: Paper no. GL-84-8: Geotechnical Lab, USAE Waterways Experiment Station, Vicksburg, Mississippi, 75 p.
Miller, S. M. and Borgman, L. E., 1984, Probabilistic Characterization of Shear Strength Using Results of Direct Shear Tests: Geotechnique, v. 34, p. 273–276.
Neuman, S. P.; Feddes, R. A.; and Bresler, E., 1974, Finite Element Simulation of Flow in Saturated-Unsaturated Soils Considering Water Uptake by Plants: Hydrodynamics and Hydraulic Engineering Laboratory, Israel Institute of Technology, Haifa, Israel.
Newendorp, P. D., 1975, Decision Analysis for Petroleum Exploration: Petroleum Publishing Company, Tulsa, Oklahoma, 668 p.
Prellwitz, R. W. and Babbitt, R. E., 1984, Long-term Groundwater Monitoring in Mountainous Terrain: Paper presented at 63rd Annual Meeting of the Transportation Research Board: Washington, DC, January.
Prickett, T. A. and Lonnquist, C. G., 1971, Selected Digital Computer Techniques for Groundwater Resource Evaluation, Bull. 55: Illinois State Water Survey, Urbana, Illinois, 62 p.
Sangrey, D. A.; Harrop-Williams, K. O.; and Klaiber, J. A., 1984, Predicting Groundwater Response to Precipitation: Jour. Geotech. Eng. ASCE, v. 110, p. 957–975.
Soong, T. T., 1981, Probabilistic Modeling and Analysis in Science and Engineering: John Wiley & Sons, New York, 384 p.
Ward, T. J.; Li, R. M.; and Simons, D. B., 1979, Mathematical Modeling Approach for Delineating Landslide Hazards in Watersheds,in Proceedings of the 17th Annual Symposium on Engineering Geology and Soils Engineering: Moscow, Idaho, p. 109–142.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Miller, S.M. A temporal model for landslide risk based on historical precipitation. Math Geol 20, 529–542 (1988). https://doi.org/10.1007/BF00890335
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00890335