Abstract
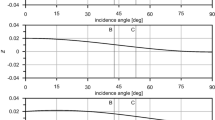
Biot's theory is employed to study the reflection and transmission ofSH waves in a sandy layer lying over a fluid-saturated porous solid half-space. The entire medium is considered under constant initial stress. Effects of sandiness, initial stress, anelasticity and viscosity of the interstitial fluid on the partitioning of energy are studied. In the presence of initial stress the incident wave starts attenuating when incider beyond a certain angle (depending upon the amount of initial stress), even if the medium is perfectly clastic. Anelasticity of the solid layer results in the dissipation of energy during transmission. The direction of attenuation vector of incident wave affects the dissipation energy to a large extent. Effect on partitioning of energy reverse at incidence after the critical angle. A complete account of energy returmed back to the underlying half-space and that which is dissipated in the overlying layer has been discussed analytically as well as numerically.
Similar content being viewed by others
References
Abramowitz, M., andStegun, I. A.,Handbook of Mathemaical Functions (Dover Publications, New York 1965).
Achenbach, J. D.,Weve Propagation in Elastic Solids (North-Holland Publishing Company, Amsterdam 1973).
Bior, M. A. (1956),Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid, J. Acoust. Soc. Am.28, 168–191.
Borcherdt, R. D. (1982),Reflection-refraction of General P and Type-1 S Waves in Elastic and Anelastic Solids, Geophys. J. R. Astr. Soc.70, 621–638.
Deresiewicz, H. (1960),The Effect of Boundaries on Wave Propagation in a Liquid-filled Porous Solid — I. Reflection of Plane Waves at a Free Plane Boundary, Bull. Seismol. Soc. Am.50, 599–607.
Deresiewicz, H. (1964),The Effect of Boundaries on Wave Propagation in a Liquid-filled Porous Solid — XI. Waves in a Plate, Bull. Seismol. Soc. Am.64, 1901–1907.
Deresiewicz, H., andLevy, A. (1967).The Effect of Boundaries on Wave Propagation in a Liquid-filled Porous Solid — X. Transmission through a Stratified Medium, Bull. Seismol. Soc. Am.57, 381–391.
Deresiewicz, H., andRice, J. T. (1962),The Effect of Boundaries on Wave Propagation in a Liquid-filled Porous Solid — III. Reflection of Plane Waves at a Free Plane Boundary (General Case), Bull. Seismol. Soc. Ar.52, 599–625.
Deresiewicz, H., andSkalak, R. (1963),On Uniqueness in Dynamic Poroelasticity, Bull. Seismol. Soc. Am.63, 783–789.
Hajra, S., andMukhopadhyay, A. (1982),Reflection and Refraction of Seismic Waves Incident Obliquely at the Boundary of Liquid Saturated Porous Solid, Bull. Seismol. Soc. Am.72, 1509–1533.
Krebes, E. S. (1983),The Viscoelastic Reflection/Transmission Problem: Two Special Cases, Bull. Seismol. Soc. Am.73, 1673–1683.
Schmitt, D. P. (1989),Acoustic Multipole Logging in Transversely Isotropic Poroelastic Formations, J. Acoust. Soc. Am.64, 1125–1131.
Sharma, M. D., andGogna, M. L. (1991),Propagation of Love Waves in an Initially Stressed Medium Consisting of Slov Elastic Layer Lying over a Liquid Saturated Porous Solid Half-space, J. Acoust. Soc. Am.89, 2584–2588.
Yew, C. H., andJogi, P. N. (1976),Study of Wave Motions in Fluid-saturated Porous Rocks, J. Acoust. Soc. Am.60, 2–8.
Yew, C. H., andWeng, X. (1987),A Study of Reflection and Refraction of Waves at the Interface of Water and Porons Sea Ice J. Acoust. Soc. Am.82, 342–353.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Sharma, M.D., Gogna, M.L. Reflection and transmission ofSH waves in an initially stressed medium consisting of a sandy layer lying over a fluid-saturated porous solid. PAGEOPH 140, 613–628 (1993). https://doi.org/10.1007/BF00876579
Received:
Revised:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00876579