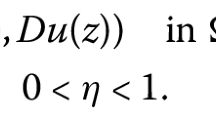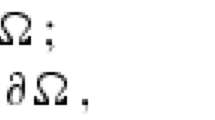Skip to main content
SpringerLink
Log in

Solution of a Dirichlet problem in a crescent-shaped domain

  • Published:
Journal of engineering physics Aims and scope

Abstract

We present a solution of a Dirichlet problem for the Laplace equation in a crescentshaped domain and apply this solution to some stationary problems of heat conduction, electrostatics, and the theory of elasticity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature cited

  1. V. I. Vlasov and A. P. Prudnikov, “Asymptotics of the solutions of some problems for the Laplace equation with deformation of a domain,” in: Modern Problems of Mathematics, Vol. 20 [in Russian] (Advances in Science and Engineering, VINITI, Academy of Sciences of the USSR), Moscow (1982), pp. 3–36.

    Google Scholar 

  2. Ya. S. Uflyand, Bipolar Coordinates in the Theory of Elasticity [in Russian], GITTL, Moscow-Leningrad (1950).

    Google Scholar 

  3. Hu Hai-Chang, “Torsion of prisms bounded by two intersecting circular cylinders,” Acta Phys. Sinica,9, No. 4, 238–254 (1953).

    Google Scholar 

  4. T. H. Gronwall, “On the influence of keyways of the stress distribution in cylindrical shafts,” Trans. Am. Math. Soc.,20, No. 3, 234–244 (1919).

    Google Scholar 

  5. S. P. Timoshenko, Theory of Elasticity, McGraw-Hill, New York (1934).

    Google Scholar 

  6. I. S. Sokolnikoff and E. S. Sokolnikoff, “Torsion of regions bounded by circular arcs,” Bull. Am. Math. Soc.,44, No. 3, 384–387 (1938).

    Google Scholar 

  7. Ya. I. Burak, Some Problems of Torsion in the Bending of Prismatic Rods [in Ukrainian], Vid. Akad. Nauk UkrRSR, Kiev (1959).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computing Center, Academy of Sciences of the USSR, Moscow

    V. I. Vlasov

Authors
  1. V. I. Vlasov
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 50, No. 6, pp. 1024–1031, June, 1986.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vlasov, V.I. Solution of a Dirichlet problem in a crescent-shaped domain. Journal of Engineering Physics 50, 741–747 (1986). https://doi.org/10.1007/BF00871551

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00871551

Keywords

Search

Navigation