Understanding the meaning of the shunt fraction calculation

Abstract

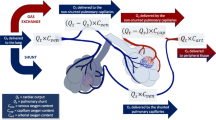
The pulmonary shunt fraction (${{\dot Qs} \mathord{\left/ {\vphantom {{\dot Qs} {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}}$) is frequently calculated in critically ill patients to monitor the effectiveness of pulmonary oxygenation. The breathing of pure oxygen often results in higher calculated${{\dot Qs} \mathord{\left/ {\vphantom {{\dot Qs} {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}}$ values that have been attributed to the development of atelectasis, ventilation-perfusion imbalance, or both. To interpret properly the changes in calculated${{\dot Qs} \mathord{\left/ {\vphantom {{\dot Qs} {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}}$ that occur when the inspired oxygen fraction is altered, the changes produced in all the variables affecting${{\dot Qs} \mathord{\left/ {\vphantom {{\dot Qs} {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}}$ must be known. This tutorial presents an in-depth analysis of the four variables affecting the calculation of${{\dot Qs} \mathord{\left/ {\vphantom {{\dot Qs} {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}}$ $\dot Vo_2$ (oxygen uptake),$\dot Qt$ (cardiac output), Cc'O₂(oxygen content in pulmonary end capillaries), and$C\bar vO_2$ (oxygen content in mixed venous blood). These variables are related according to the following equation, which derived by combining the Fick and the classic shunt equations:${{\dot Qs} \mathord{\left/ {\vphantom {{\dot Qs} {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}} = 1 - [({{{{\dot Vo_2 } \mathord{\left/ {\vphantom {{\dot Vo_2 } {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}})} \mathord{\left/ {\vphantom {{{{\dot Vo_2 } \mathord{\left/ {\vphantom {{\dot Vo_2 } {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}})} {(Cc'O_2 }}} \right. \kern-\nulldelimiterspace} {(Cc'O_2 }} - C\bar vO_2 )]$. Three-dimensional surface representations relating these variables are also presented to help the reader understand the effects of these variables on the calculated${{\dot Qs} \mathord{\left/ {\vphantom {{\dot Qs} {\dot Qt}}} \right. \kern-\nulldelimiterspace} {\dot Qt}}$.