Abstract
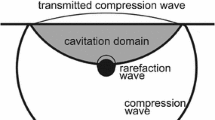
The problem of the development of the cavitation zone and the rarefaction wave profile in the region of regular reflection of the spherical shock wave of an underwater explosion from a free surface is analyzed for the axisymmetric formulation within the framework of a model of the two-phase medium consisting of a liquid with cavitation nuclei of the free gas uniformly distributed in it. An example of the calculation of the rarefaction wave profile and the zone of visible cavitation at different times is given for the case of the explosion of 1-g charge at depths of 3 and 5.3 cm for an initial volumetric gas concentration of 10−11 and an initial cavitation nucleus radius of 5 · 10−5 cm. The results of the calculation are compared with experiment.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
B. D. Khristoforov, “Interaction of a shock wave in water with the free surface,” Zh. Prikl. Mekh. Tekh. Fiz., No. 1 (1961).
A. A. Grib, A. G. Ryabinin, and S. A. Khristianovich, “Reflection of a plane shock wave from a free surface in water,” Prikl. Mat. Mekh.,20, No. 4 (1956).
B. I. Zaslavskii, “Nonlinear interaction between the free surface and a spherical shock wave produced by the explosion of a submerged charge,” Zh. Prikl. Mekh. Tekh. Fiz., No. 4 (1964).
M. Dubesset and M. Laverge, “Calcul de la cavitation due aux explosions sous-marines a faible profondeur,” Acustica,20, No. 5 (1968).
R. A. Wentzell, H. D. Scott, and R. P. Chapman, “Cavitation due to shock pulses reflected from the sea surface,” Acoust. Soc. Amer.,46, No. 3 (Part 2) (1969).
B. V. Zamyshlyaev and Yu. S. Yakovlev, Dynamic Loads near an Underwater Explosion [in Russian], Sudostroenie, Leningrad (1967).
L. I. Briggs, “Limiting negative pressure of water,” J. Appl. Phys.,21, No. 7 (1950).
L. R. Gavrilov, “Free gas content in liquids and methods of its measurement,” in: The Physics and Technology of Powerful Ultrasound and the Physical Bases of Ultrasonic Technology [in Russian], Part 4 (1970).
D. Y. Hsieh, “Bubble growth in viscous liquid due to a transient pulse,” ASME Paper 70-FE-5 for Meeting of May 24–27 (1970).
B. Persson, “On the bounds for the threshold pressure initiating bubble growth,” J. Fluids Eng., Trans. ASME,95, Ser. 1, No. 1, 98–102 (1973).
V. K. Kedrinskii, “Propagation of disturbances in a liquid containing gas bubbles,” Zh. Prikl. Mekh. Tekh. Fiz., No. 4 (1968).
L. W. Hantel and W. S. Davis, “Spherical explosions in water,” in: Fifth Symposium on Detonation, Pasadena, California, August 18–21 (1970).
S. V. Iordanskii, “Equations of motion of a liquid containing gas bubbles,” Zh. Prikl. Mekh. Tekh. Fiz., No. 3 (1960).
B. S. Kogarko, “One model for a cavitating liquid,” Dokl. Akad. Nauk SSSR,137, No. 6 (1961).
L. van Wijngaarden, “Onthe equation of motion for mixtures of gas bubbles in liquid,” J. Fluid Mech.,33, No. 3, 465 (1968).
B. D. Khristoforov, “Parameters of the shock wave and of a gas bubble during the underwater explosion of PETN charges of small weight,” Zh. Prikl. Mekh. Tekh. Fiz., No. 2 (1960).
Author information
Authors and Affiliations
Additional information
Translated from Zhurnal Prikladnoi Mekhaniki i Tekhnicheskoi Fiziki, No. 5, pp. 68–78, September–October, 1975.
Rights and permissions
About this article
Cite this article
Kedrinskii, V.K. Dynamics of the cavitation zone during an underwater explosion near a free surface. J Appl Mech Tech Phys 16, 724–733 (1975). https://doi.org/10.1007/BF00854082
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00854082