Oscillation of flat layered shells with local elastic supports

Abstract

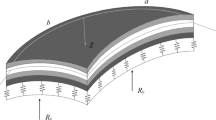
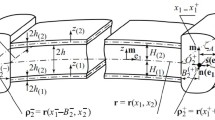
The study of oscillation in thin-walled construction elements on elastic supports is of great practical interest. Various aspects of the problems of mechanics arising in this regard have been considered by many authors, especially in recent years. The authors of [4, 8, 13, 14, 17–19, 22] have presented voluminous graphical and tabular material for solid beams with elastic supports and for rectangular plates supported on rigid point supports along the edges and in the inner area; moreover, the authors of [22] present results relating to linear supports and circular plates, while in [5, 13, 18, and 22] the results reported have to do with the forms of the fundamental oscillation. In [5] the elastic bond is modelled by means of a Vinkperovskii foundation with a discontinuous bed coefficient. Cylindrical shells are examined in [1, 6], while in [21], for a spherical shell with elastic supports, an analytical solution is constructed. The authors of [23, 24] investigate the effect of an attached mass and a linear support for a circular and a rectangular plate, and a comparison with experimental data is made for a lower frequency. The close connection between the problems in question with those involving oscillation of shells with attached masses is reflected in [3, 7, 11, 16]. Analysis of the results obtained in the works mentioned above and in others shows that, unlike the case of beam systems, numerical results for plates and shells are significantly more difficult to obtain. Therefore, in the overwhelming majority of publications, thin plates and shells are examined, while to describe the process of their deformation classical models are used; here the supports, as a rule, are assumed to be absolutely rigid. The oscillation of anisotropic and, in particular, layered construction elements on elastic supports with further consideration of the bending rigidity of the latter clearly has not been studied sufficiently, which makes further research in this field timely. The present article examines layered, flat, orthotropic shells on a rectilinear layout, for which a solution of the static problem has been obtained previously [9, 10]. The basic assumptions of the computation method, developed for calculating the stress-deformed state (SDS) arising during driven oscillation of these objects far from the resonance points, as well as for determining the fundamental oscillation frequencies (FOF), are presented. Unlike traditional approaches, this method realizes the possibility of calculating, along with the normal reactions of elastic supports, reactive moments and tangential forces; in describing the movement of the system, the relations of the improved theory of shells are used [2].