Summary
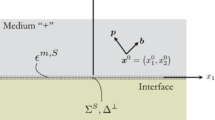
Analytical closed-form solutions are proposed in a rather compact form for the stress and displacement fields induced by out-of-plane loading of a semi-infinite anisotropic material with inclined strata. The solutions are then extended to include the case of a bimaterial with a planar interface. Several boundary conditions are considered for the interface which may be between two anisotropic half-planes with different elastic properties, or two different orientations of the strata in the same material.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Jedidi, A.; Hirashima, K.; Mura, T.: Analytical solutions for anisotropic bimaterials under several boundary conditions on the interface. Arch. Appl. Mech. 65 (1995) (in print)
Lin, W.; Honein, T.; Herrmann, G.: A novel method of stress analysis of elastic materials with damage zones. In: Boehler, J. P. (ed.) Yielding, damage and failure of anisotropic solids, pp. 609–615. London: Mech. Eng. Publications
Lekhnitskii, S. G.: Theory of elasticity of an anisotropic elastic body. San Francisco: Holden-Day (1963)
Mossakowski, J.: The Michell problem for anisotropic semi-infinite plate. In: Proc. 9th Int. Cong. Appl. Mech. 6 (1957) 57–66
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Jedidi, A., Hirashima, K., Yao, C. et al. Out-of-plane loading of anisotropic bimaterials and semi-infinite materials. Arch. Appl. Mech. 65, 76–85 (1995). https://doi.org/10.1007/BF00787901
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00787901