Summary
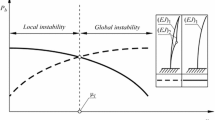
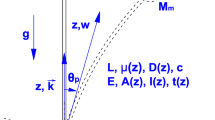
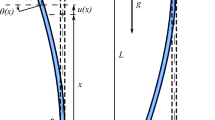
The critical load of the divergence instability, eigenfrequency curves and the Rayleigh's quotient for a column with one clamped end, subject to a generalized load, have been established in the paper. In particular, it has been found that the way the external force is being applied results in the linear dependence of both the shearing force and the bending moment upon both the deflection and the deflection angle of the loaded end. Such a case of loading exists e.g. for a column which supports a transversally stabilized structure when the contact surfaces are cylindrical. Furthermore, it has been theoretically and experimentally proven, that the slope of some eigencurves can change from positive to negative with the increasing load value.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Leipholz, H. H. E.: On conservative elastic systems of the first and second kind. Ing. Arch. 43 (1974) 255–271
Huseyin, K.: Pseudo-conservative systems. In: Leipholz, H. H. E. (ed.) Vibrations and Stability of Multiple Parameter Systems, pp. 91–111. Alphen Aan den Rijn: Noordhoff International Publishing 1978
Gajewski, A.: Vibration mode shapes of the compressing bars under nonconservative loading (in polish). Czasopismo Techniczne 141 (1970) 1–8
Kordas, Z. Stability of the elastically clamped compressed bar in the general case of behaviour of the loading. Bulletin de L'Academie Polonaise des Sciences XI (1963) 419–427
Gajewski, A.;Życzkowski, M. Optimal structural design under stability constraints, pp. 103–107. Dordrecht: Kluwer Academic Publishers 1988
Gajewski, A.;Życzkowski, M. Optimal design of elastic columns subject to the general conservative behaviour of loading. Z. Angew. Math. Phys. 21 (1970) 806–818
Washizu, K. Variational methods in elasticity and plasticity, pp. 144–146. Oxford: Pergamon Press 1974
Leipholz, H. H. E. Aspects of dynamic stability of structures. Proc. ASCE/Eng. Mech. Division 101 (1975) 109–124
Xiong, Y.;Tabarrok, B. A note on the dynamic behaviour of discretized non-conservative systems. J. Sound Vib. 162 (1962) 429–439
Bogacz, R.; Mahrenholtz, O.: Modal analysis in application to design of inelastic structures subjected to circulatory loading. In: Proc. of the Euromech Colloquium 174, on Inelastic Structures under Variable Loads, Palermo, 1983, pp. 377–388
Danielski, J.;Mahrenholtz, O. Vergleich theoretischer und experimentaller Ergebnisse eines gestützten Beck-Reut-Stabes. Z. Angew. Math. Mech. 71 (1991) T186-T189
Tomski, L.; Golebiowska-Rozanow, M.; Przybylski, J.; Szmidla, J.: Stability and vibration of a two-member frame under generalised load. In: Proc. of the European Session of the Int. Colloquium on Stability of Steel Structures, Budapest, 1995, I409–I416
Dąbrowski, R. Stability of a freestanding column loaded through a roller bearing. Ing. Arch. 54 (1984) 16–24
Sundararajan, C. On the flutter and divergence of a two-degree-of-freedom elastic system subjected to follower forces. Z. Angew. Math. Mech. 53 (1973) 801–802
Moon, P.;Spencer, D. E. Field theory for engineers, pp. 92–120 (Polish edition). Warszawa: PWN 1966
Author information
Authors and Affiliations
Additional information
This research has been supported by the State Committee for Scientific Research, Warsaw, Poland, 1995.
Rights and permissions
About this article
Cite this article
Tomski, L., Przybylski, J., Gołębiowska-Rozanow, M. et al. Vibration and stability of an elastic column subject to a generalized load. Arch. Appl. Mech. 67, 105–116 (1996). https://doi.org/10.1007/BF00787144
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00787144