Summary
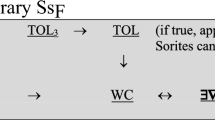
This approach does not define a probability measure by syntactical structures. It reveals a link between modal logic and mathematical probability theory. This is shown (1) by adding an operator (and two further connectives and constants) to a system of lower predicate calculus and (2) regarding the models of that extended system. These models are models of the modal systemS 5 (without the Barcan formula), where a usual probability measure is defined on their set of possible worlds. Mathematical probability models can be seen as models ofS 5.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bigelow, J. C.: 1976, ‘Possible Worlds Foundations for Probability’,Journal of Philosophical Logic 5, 297–320.
Bigelow, J. C.: 1977, ‘Semantics of Probability’,Synthese 36, 459–471.
Burgess, J. P.: 1969, ‘Probability Logic’,Journal of Symbolic Logic 2, 264–274.
Dempster, A. P.: 1966, ‘New Methods for Reasoning Towards Posterior Distributions Based on Samples’,Annals of Mathematical Statistics 34, 355–374.
Dempster, A. P.: 1967, ‘Upper and Lower Probabilities Induced by a Multivalued Mapping”,Annals of Mathematical Statistics 38, 325–339.
Dempster, A. P.: 1968, ‘A Generalization of Bayesian Inference’,Journal of the Royal Statistical Society 30, 205–247.
Fenstad, E.: 1969, ‘The Structure of Logical Probabilities’,Synthese 18, 1–23.
Fenstad, E.: 1980, ‘The Structure of Probabilities Defined on First-order Languages’, in Jeffrey, R. C. (ed.),Studies in Inductive Logic and Probability, II, University of California Press, Berkeley.
Fisher, R. A.: 1950,Contributions to Mathematical Statistics, John Wiley & Sons Inc., Chapman and Hall, New York.
Fisher, R. A.: 1956,Statistical Methods and Scientific Inference, Oliver and Boyd, London.
Giere, R. N.: 1973, ‘Objective-Single Case Probability and the Foundations of Statistic’, in: Suppes, P., Henkin, L., Joja, A., and Moisil, Gr. C. (eds.),Logic, Methodology and Philosophy of Science IV, North-Holland Publishing Company, Amsterdam, pp. 467–483.
Giere, R. N.: 1976, ‘A Laplacean Formal Semantics for Single Case Propensities’,Journal of Philosophical Logic 5, 321–359.
Hughes, G. E. and Cresswell, M. J.: 1968,An Introduction to Modal Logic, Methuen, London.
Matheron, G.: 1975,Random Sets and Integral Geometry, John Wiley & Sons Inc., New York, London.
Niiniluoto, I.: 1981, ‘Statistical Explanation Reconsidered’,Synthese 48, 437–472.
Niiniluoto, I.: 1988, ‘Probability, Possibility and Plenitude’, in: Fetzer, J. H. (ed.),Probability and Causality, D. Reidel Publishing Company, Dodrecht, pp. 91–108.
Popper, K.: 1959, ‘The Propensity Interpretation of Probability’,British Journal of Philosophy of Science 10, 25–42.
Shafer, G.: 1976,Mathematical Theory of Evidence, Princeton-University Press, Princeton.
Walley, P., Fine, T.: 1979, ‘Varieties of Modal (Classificatory) and Comparative Probability’,Synthese 41, 321–374.
Walley, P., Fine, T.: 1982, ‘Towards a Frequency Approach of Upper and Lower Probability’,The Annals of Statistic 10, 741–761.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Schneider, C. Probability: A new logico-semantical approach. J Gen Philos Sci 25, 107–124 (1994). https://doi.org/10.1007/BF00769280
Issue Date:
DOI: https://doi.org/10.1007/BF00769280