Skip to main content
SpringerLink
Log in

Temperature stresses in a heat-sensitive ceramic plate

  • Scientific-Technical Section
  • Published:
Strength of Materials Aims and scope

Abstract

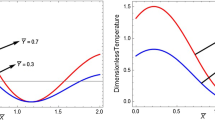
The quasistatic thermoelastic state of a rectangular ceramic plate freely supported around the perimeter is discussed. The problem is reduced to the solution of a system of nonlinear inhomogeneous integrodifferential equations consisting of a nonlinear differential heat-conduction equation with allowance for the temperature dependence of the thermophysical characteristics of the material and an integrobiharmonic equation characterizing the plate's deflection. The expression for the components of the temperature stresses caused by a nonlinear temperature field are derived in the form of ternary series. The thermoelastic state is calculated for a rectangular backing-type plate produced from the commercial ceramic VK 94-1.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature cited

  1. A. A. Shternov, Physical Bases of the Construction And Technology of REA And Microelectronics [in Russian], Radio i Svyaz', Moscow (1981).

    Google Scholar 

  2. K. Okadzaki, Ceramic Dielectric Technology [Russian translation], Énergiya, Moscow (1976).

    Google Scholar 

  3. R. L. Balkevich, Commercial Ceramics [in Russian], Stroiizdat, Moscow (1984).

    Google Scholar 

  4. N. I. Kalynyak and B. I. Kalynyak, Nonlinear Heat Condition Problems [in Russian], Moscow (1977). Deposited in the All-Union Center for Scientific And Technical information on October 6, 1977.

  5. M. I. Kalinyak, “Asymptotic method of solving the quasistatic differential heat-conduction equation,” Visn. L'viv. Politekh. Inst., No. 44, 133–145 (1970).

    Google Scholar 

  6. N. I. Kalynak and O. V. Trush, Problem of Nonlinear Heat Conduction Under Given Initial and Nonlinear Boundary Conditions [in Russian], Moscow (1978). Deposited in the All-Union Center for Scientific And Technical Information on September 12, 1978.

  7. N. I. Kalynyak, Problem of Nonlinear Heat Conduction for a Rectangular Plate [in Russian], Moscow (1981). Deposited in the All-Union Center for Scientific And Technical Information on May 25, 1981.

  8. N. I. Kalynyak and R. V. Gladysh, Nonlinear Temperature Field in a Rectangular Plate With Similar Conditions on Its Surface [in Russian], Moscow (1985). Deposited in the All-Union Center for Scientific And Technical Information on December 17, 1985.

  9. S. P. Timoshenko, Course in Elasticity Theory [in Russian], Naukova Dumka, Kiev (1985).

    Google Scholar 

  10. L. A. Kozdoba and V. L. Chumakov, “Use of the small-parameter method to solve the heat-conduction problem with temperature-dependent heat sources,” Inzh.-Fiz. Zh.,22, No. 1, 161 (1985).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. L'vov

    N. I. Kalynyak, R. V. Gladysh, V. A. Volos & I. E. Kainskii

Authors
  1. N. I. Kalynyak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. V. Gladysh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. A. Volos
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. I. E. Kainskii
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Problemy Pochnosti, No. 10, pp. 88–93, October, 1990.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kalynyak, N.I., Gladysh, R.V., Volos, V.A. et al. Temperature stresses in a heat-sensitive ceramic plate. Strength Mater 22, 1503–1511 (1990). https://doi.org/10.1007/BF00767240

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00767240

Keywords

Search

Navigation